Sex and Rate Change Differences in QT/RR Hysteresis in Healthy Subjects
- PMID: 35197861
- PMCID: PMC8859307
- DOI: 10.3389/fphys.2021.814542
Sex and Rate Change Differences in QT/RR Hysteresis in Healthy Subjects
Abstract
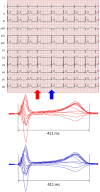
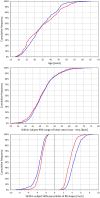
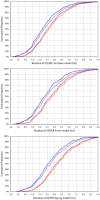
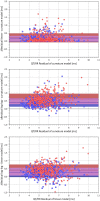
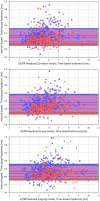
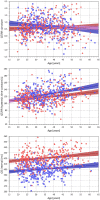
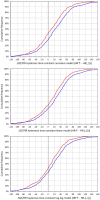
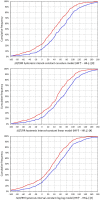
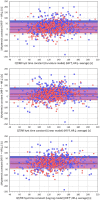
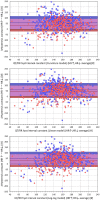
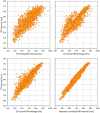
While it is now well-understood that the extent of QT interval changes due to underlying heart rate differences (i.e., the QT/RR adaptation) needs to be distinguished from the speed with which the QT interval reacts to heart rate changes (i.e., the so-called QT/RR hysteresis), gaps still exist in the physiologic understanding of QT/RR hysteresis processes. This study was designed to address the questions of whether the speed of QT adaptation to heart rate changes is driven by time or by number of cardiac cycles; whether QT interval adaptation speed is the same when heart rate accelerates and decelerates; and whether the characteristics of QT/RR hysteresis are related to age and sex. The study evaluated 897,570 measurements of QT intervals together with their 5-min histories of preceding RR intervals, all recorded in 751 healthy volunteers (336 females) aged 34.3 ± 9.5 years. Three different QT/RR adaptation models were combined with exponential decay models that distinguished time-based and interval-based QT/RR hysteresis. In each subject and for each modelling combination, a best-fit combination of modelling parameters was obtained by seeking minimal regression residuals. The results showed that the response of QT/RR hysteresis appears to be driven by absolute time rather than by the number of cardiac cycles. The speed of QT/RR hysteresis was found decreasing with increasing age whilst the duration of individually rate corrected QTc interval was found increasing with increasing age. Contrary to the longer QTc intervals, QT/RR hysteresis speed was faster in females. QT/RR hysteresis differences between heart rate acceleration and deceleration were not found to be physiologically systematic (i.e., they differed among different healthy subjects), but on average, QT/RR hysteresis speed was found slower after heart rate acceleration than after rate deceleration.
Keywords: QT/RR adaptation; QT/RR hysteresis; age influence; best-fit models; healthy subjects; non-linear regression modelling; sex differences.
Copyright © 2022 Andršová, Hnatkova, Šišáková, Toman, Smetana, Huster, Barthel, Novotný, Schmidt and Malik.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures
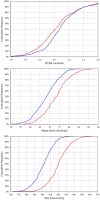
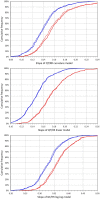
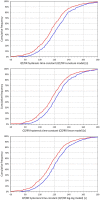
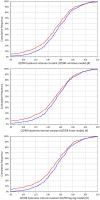
References
-
- Axelsson K. J., Gransberg L., Lundahl G., Vahedi F., Bergfeldt L. (2021). Adaptation of ventricular repolarization time following abrupt changes in heart rate: comparisons and reproducibility of repeated atrial and ventricular pacing. Am. J. Physiol. Heart Circ. Physiol. 320, H381–H392. 10.1152/ajpheart.00542.2020 - DOI - PubMed
-
- Bauer A., Klemm M., Rizas K. D., Hamm W., von Stülpnagel L., Dommasch M., et al. (2019). Prediction of mortality benefit based on periodic repolarisation dynamics in patients undergoing prophylactic implantation of a defibrillator: a prospective, controlled, multicentre cohort study. Lancet 394, 1344–1351. 10.1016/S0140-6736(19)31996-8 - DOI - PubMed
LinkOut - more resources
Full Text Sources

