Accumulation of Particles and Formation of a Dissipative Structure in a Nonequilibrium Bath

Abstract

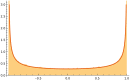
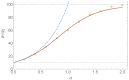
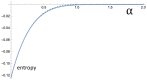
The standard textbooks contain good explanations of how and why equilibrium thermodynamics emerges in a reservoir with particles that are subjected to Gaussian noise. However, in systems that convert or transport energy, the noise is often not Gaussian. Instead, displacements exhibit an α-stable distribution. Such noise is commonly called Lévy noise. With such noise, we see a thermodynamics that deviates from what traditional equilibrium theory stipulates. In addition, with particles that can propel themselves, so-called active particles, we find that the rules of equilibrium thermodynamics no longer apply. No general nonequilibrium thermodynamic theory is available and understanding is often ad hoc. We study a system with overdamped particles that are subjected to Lévy noise. We pick a system with a geometry that leads to concise formulae to describe the accumulation of particles in a cavity. The nonhomogeneous distribution of particles can be seen as a dissipative structure, i.e., a lower-entropy steady state that allows for throughput of energy and concurrent production of entropy. After the mechanism that maintains nonequilibrium is switched off, the relaxation back to homogeneity represents an increase in entropy and a decrease of free energy. For our setup we can analytically connect the nonequilibrium noise and active particle behavior to entropy decrease and energy buildup with simple and intuitive formulae.

Keywords: Lévy noise; active particles; dissipative structures; entropy production; nonequilibrium thermodynamics.

Figure A1

A Lévy walk in a confined domain. Whenever the particle hits the confinement wall, it comes to a standstill there. The 1D steady-state probability distribution (a) is solved in Ref. [23]: $p_{st}\left(r\right)\propto {\left(1-r^2\right)}^{\alpha /2-1}$. Between any two small intervals along the 1D domain, steady state implies $p\left(r_1\right)k_{12}=p\left(r_2\right)k_{21}$, where the k’s denote transition rates. In 2D (b) there is circular symmetry. If we take any narrow bar through the origin and look exclusively at traffic inside that bar, $p_{st}\left(r\right)\propto {\left(1-r^2\right)}^{\alpha /2-1}$ applies again. Next, we take a state $R_3$ outside the bar (c) and include transitions between $r_1$ and $r_2$ that go via any area $R_3$. As the circular symmetry implies the absence of vortices, transitions $k_{12}^{\prime }$ and $k_{21}^{\prime }$ that go via $R_3$ must also follow $p\left(r_1\right)k_{12}^{\prime }=p\left(r_2\right)k_{21}^{\prime }$. From here it follows that $p_{st}\left(r\right)\propto {\left(1-r^2\right)}^{\alpha /2-1}$ also applies to higher dimensional setups. See the text of this Appendix for more detail.

Figure 1

Random walk in a circular domain. Whenever the particle hits the wall, it comes to a standstill and later only moves again when a computed step leads to a movement inside the circle. For every step, the direction is picked randomly and the displacement is drawn from a (a) Gaussian distribution or from a (b) Lévy-stable distribution. The circle has a radius of 20. Both distributions are symmetric around zero. The Gaussian distribution has a standard deviation of $\sqrt{2}$. For the Lévy-stable distribution, we have $\alpha =1$ and a scale factor of $\sigma =1$.

Figure 2

A Lévy walk on the interval $-1\le x\le 1$ (cf. Equation (3)). The value of the stability index is $\alpha =0.8$. Whenever the particle hits $x=\pm 1$, it stays there until an iteration occurs in the direction away from the wall. The red curve shows the analytic solution (cf. Equation (4)). The normalized histogram is the result of a numerical simulation of Equation (3); the timestep was $\Delta t=0.001$, there were ${10}^7$ iterations, and the scale factor of the symmetric, zero-centered Lévy distribution was taken to be one.

Figure 3

Two semicircular reservoirs with a small opening between them. The system contains a large number of noisy particles. At each timestep, each particle moves in an arbitrary direction with a displacement that is drawn from a Gaussian distribution or a Lévy-stable distribution as in Figure 1a,b. If a particle hits a semicircular wall, it comes to a standstill and only moves again if a computed displacement leads to motion inside the system. If a particle hits the straight vertical wall, it bounces elastically. For Gaussian noise, the system goes to an equilibrium with equal concentration on both sides of the opening. However, when the particles are subjected to Lévy noise, the steady state has an accumulation in the smaller reservoir.

Figure 4

For the setup of Figure 3 with $R_1=10$ and $R_2=1$, we let ${\phi }_1$ and ${\phi }_2$ represent the fraction of particles in reservoir 1 and 2, respectively, at steady state. The curves depict the analytic approximations, Equation (13) (dashed) and Equation (15) (solid), of ${\phi }_1/{\phi }_2$. Each dot is the result of a stochastic simulation of 40,000 particles for $4\times {10}^5$ timesteps (with $\Delta t=0.001$) following a $2\times {10}^5$ timestep relaxation period. For the approximation according to Equation (15), we let $r_0=0.05$ and find good agreement with the result of the stochastic simulation.

Figure 5

The figure on the left depicts a steady-state distribution for 50,000 Lévy particles in a two-reservoir confinement as depicted in Figure 3 after ${10}^5$ timesteps. We have $R_1=2$, $R_2=1$, and the opening has a width $d=0.1$. For the figure on the right we started with a steady-state distribution and ran the simulation for another ${10}^5$ iterations. We took a horizontal strip through the center with a width of 0.02 and partitioned it into 300 bins. Particles in each bin were counted and the results of the subsequent ${10}^5$ iterations were added. The solid line represents the resulting normalized 1D histogram. The dashed reference curve is the solution Equation (4). For the left reservoir, the domain was scaled to a length 2. Normalization of the combination of analytic solutions was done such that the probability to be in the left reservoir is 2/3. It is readily verified that this leads to continuity at the location of the opening.

Figure 6

Given the setup of Figure 3 with $V_{tot}=1$ and $R_1=10R_2$, the curves show the entropy per particle, $s_{tot}$, as a function of the stability parameter $\alpha$ of the Lévy noise. The nonequilibrium noise leads to a concentration difference between the two reservoirs. The associated entropy decrease $s_{tot}$ is obtained by substituting into Equation (19) the approximate ratio according to Equation (13) (dashed curve) and according to Equation (15) (solid curve). For Equation (15) we took $r_0=0.05$, i.e., the value that led to good agreement with the stochastic stimulation (cf. Figure 4).