Quantum-Classical Entropy Analysis for Nonlinearly-Coupled Continuous-Variable Bipartite Systems

Abstract

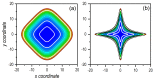
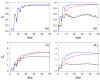
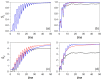
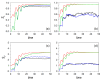
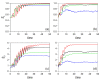
The correspondence principle plays a fundamental role in quantum mechanics, which naturally leads us to inquire whether it is possible to find or determine close classical analogs of quantum states in phase space-a common meeting point to both classical and quantum density statistical descriptors. Here, this issue is tackled by investigating the behavior of classical analogs arising upon the removal of all interference traits displayed by the Wigner distribution functions associated with a given pure quantum state. Accordingly, the dynamical evolution of the linear and von Neumann entropies is numerically computed for a continuous-variable bipartite system, and compared with the corresponding classical counterparts, in the case of two quartic oscillators nonlinearly coupled under regular and chaos conditions. Three quantum states for the full system are considered: a Gaussian state, a cat state, and a Bell-type state. By comparing the quantum and classical entropy values, and particularly their trends, it is shown that, instead of entanglement production, such entropies rather provide us with information on the system (either quantum or classical) delocalization. This gradual loss of information translates into an increase in both the quantum and the classical realms, directly connected to the increase in the correlations between both parties' degrees of freedom which, in the quantum case, is commonly related to the production of entanglement.

Keywords: Wigner distribution function; entanglement; entropy measurement; open quantum systems; quantum dynamics; quantum foundations; quantum–classical correspondence.

Figure 1

Density plots of the quartic potential for $\beta =0.01$ and two values of $\alpha$ that generate different dynamics: (a) $\alpha =0.03$ (regular dynamics) and (b) $\alpha =1$ (chaotic dynamics). From blue to red, increasing value of the potential function, black contours indicate equipotential lines at multiples of $E=15$ (last contour shown corresponds to $E=210$). White contours in both panels represent the equipotential lines for $E_0=1.5,15$, and 150, which are the energies considered in the numerical simulations here (see next sections).

Figure 2

Linear entropy (upper row panels) and von Neumann entropy (lower row panels) for an initial distribution associated with a single Gaussian wave packet at three different energies: $E_0=1.5$ (a,d), $E_0=15$ (b,e), and $E_0=150$ (c,f). The dynamics corresponds to regularity conditions, with $\alpha =0.03$. In all panels, the black line denotes the quantum results, while the red line represents the classical ones.

Figure 3

Linear entropy (upper row panels) and von Neumann entropy (lower row panels) for an initial distribution associated with a single Gaussian wave packet at three different energies: $E_0=1.5$ (a,d), $E_0=15$ (b,e), and $E_0=150$ (c,f). The dynamics corresponds to chaos conditions, with $\alpha =1$. In all panels, the black line denotes the quantum results, while the red line represents the classical ones.

Figure 4

Linear entropy (upper row panels) and von Neumann entropy (lower row panels) for an initial distribution associated with a single Gaussian wave packet moving along the channel at an energy $E_0=15$, and affected by regularity (a,c) and chaos (b,d) conditions. In all panels, the black line denotes the quantum results, the blue line represents classical motion initially oriented along the x-direction, and the red line classical motion initially directed along the y-direction.

Figure 5

Linear entropy (upper row panels) and von Neumann entropy (lower row panels) for an initial distribution associated with a single Gaussian wave packet moving along the channel at an energy $E_0=150$, and affected by regularity (a,c) and chaos (b,d) conditions. In all panels, the black line denotes the quantum results, the blue line represents classical motion initially oriented along the x-direction, and the red line classical motion initially directed along the y-direction.

Figure 6

Linear entropy (upper row panels) and von Neumann entropy (lower row panels) for an initial distribution associated with a cat state aligned along the x-channel, with an energy $E_0=15$, and affected by regularity conditions (a,c) and chaos conditions (b,d). In all panels, black line denotes the quantum results, while the red line refers to the classical ones. To compare with, the quantum and classical results for a single Gaussian distribution, with the initial at ${\mathbf{p}}_2$ (see text for details), are also included, and denoted, respectively, with the blue and green lines.

Figure 7

Linear entropy (upper row) and von Neumann entropy (lower row) for an initial distribution associated with a Bell-type entangled state for two different values of the energy, and affected by regularity conditions (a,c) and chaos conditions (b,d). Results for $E_0=15$ are denoted with the blue and green lines, respectively, for the quantum and the classical dynamical regimes. Results for $E_0=150$ are denoted with the black and red lines, respectively, for the quantum and the classical dynamical regimes.