Synthetic Spatial Foraging With Active Inference in a Geocaching Task
- PMID: 35210988
- PMCID: PMC8861269
- DOI: 10.3389/fnins.2022.802396
Synthetic Spatial Foraging With Active Inference in a Geocaching Task
Abstract
Humans are highly proficient in learning about the environments in which they operate. They form flexible spatial representations of their surroundings that can be leveraged with ease during spatial foraging and navigation. To capture these abilities, we present a deep Active Inference model of goal-directed behavior, and the accompanying belief updating. Active Inference rests upon optimizing Bayesian beliefs to maximize model evidence or marginal likelihood. Bayesian beliefs are probability distributions over the causes of observable outcomes. These causes include an agent's actions, which enables one to treat planning as inference. We use simulations of a geocaching task to elucidate the belief updating-that underwrites spatial foraging-and the associated behavioral and neurophysiological responses. In a geocaching task, the aim is to find hidden objects in the environment using spatial coordinates. Here, synthetic agents learn about the environment via inference and learning (e.g., learning about the likelihoods of outcomes given latent states) to reach a target location, and then forage locally to discover the hidden object that offers clues for the next location.
Keywords: active inference; free energy principle; geocaching; goal-directed behavior; navigation; spatial foraging; uncertainty.
Copyright © 2022 Neacsu, Convertino and Friston.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures
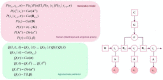



References
-
- Baranes A., Oudeyer P.-Y. (2013). Active learning of inverse models with intrinsically motivated goal exploration in robots. Rob. Auton. Syst. 61 49–73.
-
- Botvinick M., Toussaint M. (2012). Planning as inference. Trends Cogn. Sci. 16 485–488. - PubMed
LinkOut - more resources
Full Text Sources

