Arrangements of Approaching Pseudo-Lines

Abstract

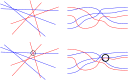
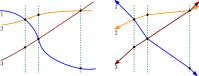
We consider arrangements of n pseudo-lines in the Euclidean plane where each pseudo-line ${\ell }_i$ is represented by a bi-infinite connected x-monotone curve $f_i\left(x\right)$ , $x\in R$ , such that for any two pseudo-lines ${\ell }_i$ and ${\ell }_j$ with $i<j$ , the function $x\mapsto f_j\left(x\right)-f_i\left(x\right)$ is monotonically decreasing and surjective (i.e., the pseudo-lines approach each other until they cross, and then move away from each other). We show that such arrangements of approaching pseudo-lines, under some aspects, behave similar to arrangements of lines, while for other aspects, they share the freedom of general pseudo-line arrangements. For the former, we prove:There are arrangements of pseudo-lines that are not realizable with approaching pseudo-lines.Every arrangement of approaching pseudo-lines has a dual generalized configuration of points with an underlying arrangement of approaching pseudo-lines. For the latter, we show:There are $2^{\Theta \left(n^2\right)}$ isomorphism classes of arrangements of approaching pseudo-lines (while there are only $2^{\Theta (nlogn)}$ isomorphism classes of line arrangements).It can be decided in polynomial time whether an allowable sequence is realizable by an arrangement of approaching pseudo-lines. Furthermore, arrangements of approaching pseudo-lines can be transformed into each other by flipping triangular cells, i.e., they have a connected flip graph, and every bichromatic arrangement of this type contains a bichromatic triangular cell.

Keywords: Discrete geometry; Order types; Pseudo-line arrangements.

Fig. 1

Vertical translation of the red lines shows that there is always a bichromatic triangle in a bichromatic line arrangement (left). For pseudo-line arrangements, a vertical translation may result in a structure that is no longer a valid pseudo-line arrangement (right)

Fig. 2

Transforming an arrangement of approaching pseudo-lines into an isomorphic one of approaching polygonal pseudo-lines

Fig. 3

A line arrangement $A_0$ (left) and the arrangements $A^{\prime }$ and $A^{\prime \prime }$ used for the transformation from A to $A_0$

Fig. 4

An approaching generalized configuration (left) and its dual approaching arrangement (right)

Fig. 5

A part of a six-element pseudo-line arrangement (bold) whose suballowable sequence (indicated by the vertical lines) is non-realizable (adapted from [, Fig. 4]). Adding the two thin pseudo-lines crossing in the vicinity of the vertical line crossed by the pseudo-lines in the order of ${\pi }_1$ and doing the same for ${\pi }_2$ enforces that the allowable sequence of any isomorphic arrangement contains the subsequence $(\mathrm{id},{\pi }_1,{\pi }_2)$

Fig. 6

A construction for an $2^{\mathrm{\Omega }(n^2)}$ lower bound on the isomorphism classes of approaching arrangements

Fig. 7

An illustration of a neighborhood of a touching point

Fig. 8

Two different arrangements induced by the same order type