Neuronal Population Transitions Across a Quiescent-to-Active Frontier and Bifurcation

Abstract

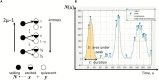
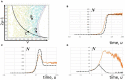
The mechanistic understanding of why neuronal population activity hovers on criticality remains unresolved despite the availability of experimental results. Without a coherent mathematical framework, the presence of power-law scaling is not straightforward to reconcile with findings implying epileptiform activity. Although multiple pictures have been proposed to relate the power-law scaling of avalanche statistics to phase transitions, the existence of a phase boundary in parameter space is until now an assumption. Herein, a framework based on differential inclusions, which departs from approaches constructed from differential equations, is shown to offer an adequate consolidation of evidences apparently connected to criticality and those linked to hyperexcitability. Through this framework, the phase boundary is elucidated in a parameter space spanned by variables representing levels of excitation and inhibition in a neuronal network. The interpretation of neuronal populations based on this approach offers insights on the role of pharmacological and endocrinal signaling in the homeostatic regulation of neuronal population activity.

Keywords: differential inclusion; epileptiform activity; excitation-inhibition balance; homeostatic regulation; neuronal avalanches.

FIGURE 1

Avalanches in the neuronal population/network. (A) The excitation by a spiking neuron with a probability μ for an excited neuron, and 1-μ for a quiescent neuron, where μ∈[1/2,1]. The excitation parameter 2μ–1 is inversely related to the information entropy of this excitation process. At maximum entropy, μ = 1/2, a neuron’s subsequent excitation is not dependent on its state. At minimum entropy, μ = 1 implying that only excited neurons can be activated by a spiking neuron. A total of N(u) spiking neurons at time u comprises x neurons that were at the excited state and y neurons at the quiescent state immediately beforehand. (B) The number of spiking neurons N for any given time u as a time-series signal. The peaks of this time series are recognized using Matlab’s findpeaks algorithm by setting the prominence to 1. The avalanche duration t is the estimate width between consecutive troughs, whereas the avalanche size S is the total area under the peak between the troughs.

FIGURE 2

Avalanche size and duration statistics in parameter space. (A) The contour plot of the extinction time with respect to the excitation parameter, 2μ–1, and global inhibition parameter, ν, for δ = 0.0005 (or δ^{– 1} = 2,000). Superimposed on the contour plot is the bifurcation locus (black curve). (B) The three-dimensional view of the contour also showing the same bifurcation locus (black curve). The color scale representing the extinction time T applies to the contour plot as well. The maximum value of T has been set to 10⁴ for faster computation, although it could have been set at a higher order of magnitude. Avalanche size (left) and duration (right) histograms, shown in double logarithmic scale, from simulations of the model with specific parameters mapped in (A). (C) 2μ–1 = 0.40, ν = 0.70. (D) 2μ–1 = 1.00, ν = 0.92. (E) 2μ–1 = 0.10, ν = 0.75. (F) 2μ–1 = 0.00, ν = 0.85. (G) 2μ–1 = 0.00, ν = 0.90. (H) 2μ–1 = 0.10, ν = 0.85.

FIGURE 3

Avalanche statistics influenced by global inhibition. The magnitude of the global inhibition parameter ν can induce different shapes of the avalanche size, f(S), and duration statistics, f(t), in double logarithmic scale, for 2μ–1 = 0.10. (A) Bimodal shape of with a tail hump for f(S) and a scaling of exponent –2, while f(t) scales as –3 at low ν. The mean duration scales with size in two regimes characterized by two exponents separated by a gap. (B) The power-law of f(S) with exponent –3/2 at critical ν with the accompanying power-law of f(t) with exponent –2. The duration scales with size with a scaling exponent of 1/2. (C) Faster tail decline at high ν for both f(S) and f(t). The scaling between duration and size with an exponent of 1/2 occurs over a limited extent.

FIGURE 4

System size effects on avalanche size statistics. Reducing the parameter effectively increases the system size relating to local inhibition. The scaling exponent (1.5) appears to be robust to the change in system size.

FIGURE 5

Convergence of stochastic solutions of the DIM. The Gillespie method covers admissible solutions that match the “mean-field” graph for different excitation and global inhibition parameters. (A) The parameter map showing the indicating parameter pairs. The stochastic solution is the average of multiple stochastic realizations (orange) and the “mean-field” solution (black dash) was estimated by numerically solving the DIM equations at the initial condition, x = 1 and y = 1. The color scale is the same as shown in Figure 2B. The number of realizations considered varied in rough proportion to the variance between realization. (B) Far from the frontier (2μ–1 = 0.6, ν = 0.6; number of realizations = 20) the stochastic solution converges to a high level of sustained number of spikes agreeing with the mean field solution. (C) Also in the interior and on the bifurcation locus (2μ–1 = 0.2, ν = 0.5; number of realizations = 84), the averaged stochastic trajectories initially ramp up and peak at a certain time before it declines and stabilizes. The peak predicted is shorter than the estimated mean field solution while the stabilization value is higher. (D) Near the frontier (2μ–1 = 0.2, ν = 0.7; number of realizations = 105), the stochastic trajectories include sustained oscillations that extend the extinction time of the population activity, which explains why the stochastic average of these trajectories substantially overshoot the peak predicted by the mean-field estimates.