Global dynamics of microbial communities emerge from local interaction rules
- PMID: 35245282
- PMCID: PMC8926250
- DOI: 10.1371/journal.pcbi.1009877
Global dynamics of microbial communities emerge from local interaction rules
Abstract
Most microbes live in spatially structured communities (e.g., biofilms) in which they interact with their neighbors through the local exchange of diffusible molecules. To understand the functioning of these communities, it is essential to uncover how these local interactions shape community-level properties, such as the community composition, spatial arrangement, and growth rate. Here, we present a mathematical framework to derive community-level properties from the molecular mechanisms underlying the cell-cell interactions for systems consisting of two cell types. Our framework consists of two parts: a biophysical model to derive the local interaction rules (i.e. interaction range and strength) from the molecular parameters underlying the cell-cell interactions and a graph based model to derive the equilibrium properties of the community (i.e. composition, spatial arrangement, and growth rate) from these local interaction rules. Our framework shows that key molecular parameters underlying the cell-cell interactions (e.g., the uptake and leakage rates of molecules) determine community-level properties. We apply our model to mutualistic cross-feeding communities and show that spatial structure can be detrimental for these communities. Moreover, our model can qualitatively recapitulate the properties of an experimental microbial community. Our framework can be extended to a variety of systems of two interacting cell types, within and beyond the microbial world, and contributes to our understanding of how community-level properties emerge from microscopic interactions between cells.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures




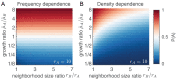
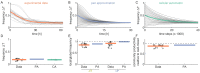
References
-
- Levin SA. Ecosystems and the Biosphere as Complex Adaptive Systems. Ecosystems. 1998;1:431–436. doi: 10.1007/s100219900037 - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

