A theoretical analysis of complex armed conflicts
- PMID: 35245318
- PMCID: PMC8896697
- DOI: 10.1371/journal.pone.0264418
A theoretical analysis of complex armed conflicts
Abstract
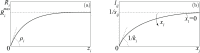
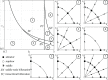
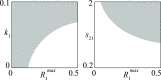
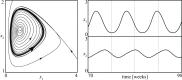
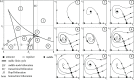
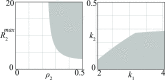
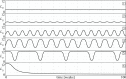
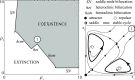
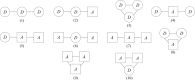
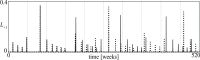
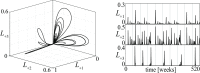
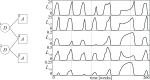
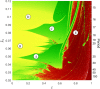
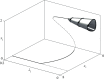
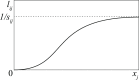
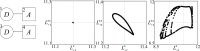
The introduction and analysis of a simple idealized model enables basic insights into how military characteristics and recruitment strategies affect the dynamics of armed conflicts, even in the complex case of three or more fighting groups. In particular, the model shows when never ending wars (stalemates) are possible and how initial conditions and interventions influence a conflict's fate. The analysis points out that defensive recruitment policies aimed at compensating for suffered losses lead to conflicts with simple dynamics, while attack groups sensitive to the damages they inflict onto their enemies can give rise to conflicts with turbulent behaviours. Since non-governmental groups often follow attack strategies, the conclusion is that the evolution of conflicts involving groups of that kind can be expected to be difficult to forecast.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
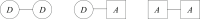






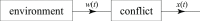
Similar articles
-
Estimating the Number of Civilian Casualties in Modern Armed Conflicts-A Systematic Review.Front Public Health. 2021 Oct 28;9:765261. doi: 10.3389/fpubh.2021.765261. eCollection 2021. Front Public Health. 2021. PMID: 34778192 Free PMC article.
-
[Protection of medical personnel in contemporary armed conflicts].Wiad Lek. 2016;69(2 Pt 2):280-4. Wiad Lek. 2016. PMID: 27487549 Polish.
-
Conflict's impact raises costs for Arctic shipping and the climate.Nature. 2022 Jun;606(7913):250. doi: 10.1038/d41586-022-01538-w. Nature. 2022. PMID: 35672513 No abstract available.
-
Use of Children as Soldiers.Pediatr Clin North Am. 2021 Apr;68(2):437-447. doi: 10.1016/j.pcl.2020.12.010. Pediatr Clin North Am. 2021. PMID: 33678297 Review.
-
Motivations for sexual violence in armed conflicts: voices from combatants in eastern Democratic Republic of Congo.Med Confl Surviv. 2021 Mar;37(1):15-33. doi: 10.1080/13623699.2021.1882365. Epub 2021 Feb 10. Med Confl Surviv. 2021. PMID: 33567882
Cited by
-
`Friend or foe' and decision making initiative in complex conflict environments.PLoS One. 2023 Feb 6;18(2):e0281169. doi: 10.1371/journal.pone.0281169. eCollection 2023. PLoS One. 2023. PMID: 36745613 Free PMC article.
References
-
- Cioffi-Revilla C Mathematical contributions to the scientific understanding of war. Formal Theories of Politics, 1989, 561–575.
-
- Cederman LE. Modeling the size of wars: From billiard balls to sandpiles. American Political Science Review, 2003, 97(1): 135–150.
-
- Rinaldi S, Della Rossa F. Conflicts among N armed groups: Scenarios from a new descriptive model. Nonlinear Dynamics 2017; 1–10
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

