A programmable qudit-based quantum processor

Abstract

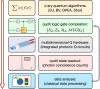
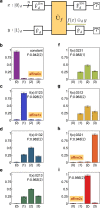
Controlling and programming quantum devices to process quantum information by the unit of quantum dit, i.e., qudit, provides the possibilities for noise-resilient quantum communications, delicate quantum molecular simulations, and efficient quantum computations, showing great potential to enhance the capabilities of qubit-based quantum technologies. Here, we report a programmable qudit-based quantum processor in silicon-photonic integrated circuits and demonstrate its enhancement of quantum computational parallelism. The processor monolithically integrates all the key functionalities and capabilities of initialisation, manipulation, and measurement of the two quantum quart (ququart) states and multi-value quantum-controlled logic gates with high-level fidelities. By reprogramming the configuration of the processor, we implemented the most basic quantum Fourier transform algorithms, all in quaternary, to benchmark the enhancement of quantum parallelism using qudits, which include generalised Deutsch-Jozsa and Bernstein-Vazirani algorithms, quaternary phase estimation and fast factorization algorithms. The monolithic integration and high programmability have allowed the implementations of more than one million high-fidelity preparations, operations and projections of qudit states in the processor. Our work shows an integrated photonic quantum technology for qudit-based quantum computing with enhanced capacity, accuracy, and efficiency, which could lead to the acceleration of building a large-scale quantum computer.

Fig. 1. The top-down hierarchy of qudit-based quantum computation.

Users can define different quantum tasks and implement different quantum algorithms in d-ary, e.g., the generalised Deutsch-Jozsa (DJ), Bernstein-Vazirani (BV), quantum phase estimation (QPEA) and Shor’s fast factorization algorithms. In the software level, a multi-qudit quantum logical circuit for executing the algorithm is compiled with single-qudit gates (e.g, Z_d, X_d and H_d) and multi-value controlled-unitary (MVCU_d) gates. In the hardware level, the logical circuit is physically implemented by an integrated photonic quantum device, i.e, the programmable d-QPU, and the gate operations are realised by optical waveguide devices, such as entangled photon sources, phase shifters, beamsplitters and interferometers. Multiple quantum tasks and algorithms can be executed, without the need of altering the device, only by reprogramming the configurations of waveguide circuits. The outcome of the hardware is given by photon coincidence counts, which are recorded and analysed by classical electronics and classical computer. Experimental outcomes can be feed-forwarded into the d-QPU for the implementation of Kitaev’s version of quantum Fourier transform algorithms.

Fig. 2. A qudit-based programmable quantum processing unit in a photonic integrated circuit chip.

a Quantum circuit, and b physical implementation of the multiqudit QPU. It bases on multiphoton multidimensional entanglement of ${∣\text{GHZ}⟩}_{n+1,d}$, where n + 1 is the number of photonic qudits and d is the local dimensionality of each qudit. _Pi is an arbitrary single-qudit gate; F_d is a generalised d-level Fourier gate; M_i is an arbitrary single-qudit projector; O_i,j (i = 1,..., n, j = 1,..., d) is an arbitrary single-qudit logic gate that is locally performed on the i-th qudit of the y-register, and the O_i,j gates are coherently entangled with the x-register state. The process of “space expansion--local operation--coherent compression" results in the multiqudit entangling gate, with a success probability of 1/d, independent on n. c The simplified schematic of a two-ququart d-QPU: (I) generation of four-level entangled state in an array of four integrated identical SFWM sources; (II) Hilbert space expansion and arbitrary single-qudit preparation of the y-register state; (III) arbitrary single-qudit operation of the x-register state; (IV) arbitrary single-qudit operation (loading in the four layers) of the y-register state, in which the operations are coherently entangled with the x-register state, thus forming the MVCU entangling gate, where the state-gate entanglement is indicated by the four colourful links; (V) coherent compression of Hilbert space by an indistinguishable erasure of spatial information; (VI) and (VII) arbitrary single-qudit projective measurement in the x and y registers. Insets: left top, measured resistance of all thermal-optic phase shifters (TOPSs); measured interference visibility of all 2-dimensional Mach-Zehnder Interferometers (MZIs); bottom right, measured classical statistic fidelities (F_c) for the Pauli X₄ gate with a mean of 0.988(13) and Fourier F₄ gate with a mean of 0.967(19). d A microscopy image of the d-QPU chip. It monolithically integrates 451 optical components, including 4 SFWM sources, 116 reconfigurable TOPS, 131 multimode interferometer (MMI) beamsplitters, 4 wavelength-division multiplexing (WDM) filters, 156 waveguide crossings and 40 grating couplers (GC). The d-QPU chip is wire bounded and can be flexibly controlled by classical electronics, and can be reliably reprogrammed and reconfigured to benchmark a spectrum of different quaternary quantum algorithms.

Fig. 3. Characterisation of quaternary multi-value controlled-unitary logic operations.

a, b Measured density matrices (ρ) for a four-level maximally entangled Bell state and a fully product state. Column heights (colours) represent absolute values ∣ρ∣ (phases Arg(ρ)) of the elements. Quantum state fidelity F_q was measured to be 0.983(4) and 0.953(3), respectively. c, Measured quantum state fidelities for a complete set of four-level Bell states ${∣\mathrm{\Psi }⟩}_{i,j}$, i, j = 0,1,2,3. The generalised Bell states are created by operating input states of $∣f_i⟩\otimes ∣k_j⟩$ in the MVCX_d gate. Shaded areas atop bars refer to ± 1σ error bars. The F_q values in a–c were estimated by Monte Carlo the photon counts with photon Poissonian statistics. d Reconstructed process matrix (χ) of the MVCX_d gate. It was measured by quantum process tomography with in total 256 quantum state tomographic measurements. We obtained the quantum process fidelity of 0.952, that is defined as Tr[χ₀χ], where χ₀ is the ideal matrix. The χ matrix is represented in the standard identity and Pauli basis {I₂, X₂, Y₂, Z₂}. Blue and red colours are used to improve the clarity. e–j Measured truth tables (normalised photon counts) for three MVCU logic gates in two complementary bases {I, II}: e, f, a multi-value controlled-X_d (MVCX_d) gate; g, h, a multi-value controlled-Z_d (MVCZ_d) gate; i, j, a multi-value controlled-H_d (MVCH_d) gate. The definitions of basis are given as: computational basis $∣k_i⟩$; Fourier basis $∣f_i⟩$; Hadamard basis $∣h_i⟩$; basis $∣l_i⟩$ is another eigenstate of the Hadamard and $∣a_i⟩$ and $∣b_i⟩$ are given by rotations, which are provided in Supplementary (i = {0, 1, 2, 3}). Classical statistic fidelities (F_c1, F_c2) are measured, which are adopted to estimate the lower and upper bound of the complementary classical fidelity: [0.891(2), 0.931(1)] for the MVCX_d, [0.912(2), 0.952(1)] for the MVCZ_d, and [0.865(1), 0.920(1)] for the MVCH_d. In e–j, the probability distributions are colour coded (key is provided at the right bottom). The values in parentheses of F_c and F_q refer to ± 1σ uncertainty from photon statistics.

Fig. 4. Implementations of generalised Deutsch-Jozsa and Bernstein-Vazirani algorithms in quaternary.

a Quantum logical circuit for implementing the d-ary Deutsch-Jozsa and Bernstein-Vazirani algorithms. This circuit can be implemented by the scheme in Fig. 1a, b with an exchange of the x and y registers. The task of the d-ary Deutsch-Jozsa algorithm is to determine an unknown multi-value function f: {0, 1,..., d−1}ⁿ → {0, 1,..., d − 1} is either constant or balanced, while that of the d-ary Bernstein-Vazirani algorithm is to compute the close expression of a multi-value affine function f: A₀ ⊕ A₁x₁. . . ⊕ A_nx_n, using only a single call of quantum oracle. When d equals to 2, the two algorithms return to the original Deutsch’s algorithms. The key part is the implementation of f(x) ⊕ _dy by the MVCU gate. The outcome of the algorithms is measured in the computation basis of the x-register states. b–i Measured probability distributions (normalised coincidence counts) of the x-register in the computational basis. Results in b–h demonstrate that the d-ary Deutsch-Jozsa algorithm allows the determination of whether f(x) is constant (b) or balanced (c–h). Results in b, c, i, h show the d-ary Bernstein-Vazirani algorithm can determine the expression of affine functions f: b, f(x) is constant and A₁=0; c, f(x) is affine and A₁=1; i, f(x) is affine and A₁=2; h, f(x) is affine and A₁=3; Dotted boxes in (b--i) refer to theoretical probability distributions. Experimental probability distributions (coloured bars) are obtained from photon coincidences, which are accumulated by 20s per measurement. The classical fidelity F_c presents the success probability of each measurement. In order to make the small error bars visible in the plots, they are plot by ± 3σ. The values in parentheses refer to ± 1σ uncertainty. All error bars are estimated from photon Poissonian statistics.

Fig. 5. Implementations of quaternary quantum phase estimation and order-finding.

a Their quantum logical circuit for implementing Kitaev’s scalable approaches. For the d-ary phase estimation, the task is to compute the eigenphase ϕ of a unitary O given its eigenstate of $∣\varphi ⟩$. For the d-ary order-finding, the task is to find the order of a function as (a^rmodN) = 1. The x-register single-qudit state is initialised by the Fourier gate F_d; the y-register is prepared in the $∣\varphi ⟩$ eigenstate (${∣0⟩}_d^{\otimes n}$ state) for phase estimation (for order-finding). The $F_d^{†}$ terminates the x-register to output the desired solution in the computational basis. In the s-th step, the Z_d rotation is added with a feedback angle of θ_s= − 0.0ϕ_s+1ϕ_s+2…ϕ_m, that is determined by previous measurements. The algorithm is iterated m times -- each step returns 1 dit result with d-ary accuracy, to obtain a m-dit estimation of the eigenphase of a unitary or the order of a function. b–d Measured probability pie-distributions of the four eigenphases (ϕ₁, ϕ₂, ϕ₃, ϕ₄) for three different unitary matrices, using the quaternary quantum phase estimation: b a generalised phase gate Z₄ as diag[$1,e^{\mathbb{i}2\pi \theta },e^{\mathbb{i}2\pi 2\theta },e^{\mathbb{i}2\pi 3\theta }$] where θ = 1/4; c a generalised Fourier gate F₄; d a random gate U_random (see form in Supplementary Note 5). Coloured sectors represent the experimental outcomes of {0,1,2,3} for each iteration, measured in the computational basis of {$∣0⟩$,$∣1⟩$,$∣2⟩$,$∣3⟩$}, respectively. The measured dominating sector is used to obtain every dit of the eigenphases; theoretical values for each dit are provided under the pies. The eigenphases are backwardly computed from the least significant dit from m = 12 to 1. e, f Measured probability distributions for the quaternary order-finding algorithm with a setting of a = 4 and a = 2, respectively. From the distributions, the order of r = 2 and r = 4 are experimentally computed with a 3-quart resolution (equivalent to 64-level), and with a classical statistic fidelity (F_c) of 0.909(9) and 0.922(9), respectively. The order-finding together with classical algorithm allows the factorisation of 15 = 3 × 5. Errors ( ± 1σ) arising from photon Poissonian noise are indicated as red shaded caps. Dashed lines refer to theoretical predictions. Experimental probability distributions in b–f are calculated from photon coincidences, which are accumulated by 20s per measurement.