A study on fractional HBV model through singular and non-singular derivatives
- PMID: 35251498
- PMCID: PMC8889534
- DOI: 10.1140/epjs/s11734-022-00460-6
A study on fractional HBV model through singular and non-singular derivatives
Abstract
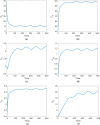
The current study's aim is to evaluate the dynamics of a Hepatitis B virus (HBV) model with the class of asymptomatic carriers using two different numerical algorithms and various values of the fractional-order parameter. We considered the model with two different fractional-order derivatives, namely the Caputo derivative and Atangana-Baleanu derivative in the Caputo sense (ABC). The considered derivatives are the most widely used fractional operators in modeling. We present some mathematical analysis of the fractional ABC model. The fixed-point theory is used to determine the existence and uniqueness of the solutions to the considered fractional model. For numerical results, we show a generalized Adams-Bashforth-Moulton (ABM) method for Caputo derivative and an Adams type predictor-corrector (PC) algorithm for Atangana-Baleanu derivatives. Finally, the models are numerically solved using computational techniques and obtained results graphically illustrated with a wide range of fractional-order values. We compare the numerical results for Caputo and ABC derivatives graphically. In addition, a new variable-order fractional network of the HBV model is proposed. Considering the fact that most communities interact with each other, and the rate of disease spread is affected by this factor, the proposed network can provide more accurate insight for the modeling of the disease.
© The Author(s), under exclusive licence to EDP Sciences, Springer-Verlag GmbH Germany, part of Springer Nature 2022.
Figures
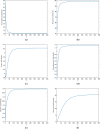
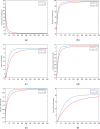
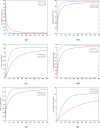
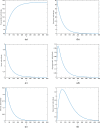
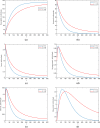
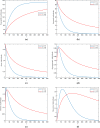
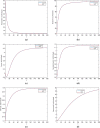
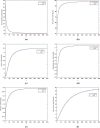


References
-
- Hoofnagle JH. Gastroenterology. 1983;84:422–424. - PubMed
-
- Fujiwara K, Yokosuka O, Ehata T, Chuang WL, Imazeki F, Saisho H, Omata M. Dig. Dis. Sci. 1998;43:368–376. - PubMed
-
- Dixit VK, Panda K, Babu AV, Kate MP, Mohapatra A, Vashistha P, Jain AK. Indian J. Gastroenterol. 2007;26:159. - PubMed
-
- Thornley S, Bullen C, Roberts M. J. Theor. Biol. 2008;254:599–603. - PubMed
-
- Mann J, Roberts M. J. Theor. Biol. 2011;269:266–272. - PubMed
LinkOut - more resources
Full Text Sources
