Adaptive optics for high-resolution imaging
- PMID: 35252878
- PMCID: PMC8892592
- DOI: 10.1038/s43586-021-00066-7
Adaptive optics for high-resolution imaging
Abstract
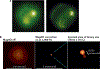
Adaptive optics (AO) is a technique that corrects for optical aberrations. It was originally proposed to correct for the blurring effect of atmospheric turbulence on images in ground-based telescopes and was instrumental in the work that resulted in the Nobel prize-winning discovery of a supermassive compact object at the centre of our galaxy. When AO is used to correct for the eye's imperfect optics, retinal changes at the cellular level can be detected, allowing us to study the operation of the visual system and to assess ocular health in the microscopic domain. By correcting for sample-induced blur in microscopy, AO has pushed the boundaries of imaging in thick tissue specimens, such as when observing neuronal processes in the brain. In this primer, we focus on the application of AO for high-resolution imaging in astronomy, vision science and microscopy. We begin with an overview of the general principles of AO and its main components, which include methods to measure the aberrations, devices for aberration correction, and how these components are linked in operation. We present results and applications from each field along with reproducibility considerations and limitations. Finally, we discuss future directions.
Conflict of interest statement
Competing interests D.T.M. and K.K. have a patent on AO-OCT technology. Both authors stand to benefit financially from any commercialization of the technology. N.J. has two patents on AO microscopy technology. M.J.B. holds patents on adaptive optics technology and has significant interests in the companies Opsydia Ltd and Aurox Ltd. Otherwise, the authors are not aware of any affiliations, memberships, funding or financial holdings that might be perceived as affecting the objectivity of this publication. K.M.H., R.T. and J.R.M. declare no competing interests.
Figures



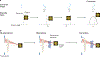






References
-
- Booth MJ Adaptive optical microscopy: the ongoing quest for a perfect image. Light. Sci. Appl. 3, e165 (2014).
-
- Ji N Adaptive optical fluorescence microscopy. Nat. Methods 14, 374–380 (2017). - PubMed
-
- Beckers JM Adaptive optics for astronomy: principles, performance, and applications. Annu. Rev. Astron. Astr. 31, 13–62 (1993).
-
- Porter J, Queener HM, Lin JE, Thorn K & Awwal A Adaptive Optics for Vision Science: Principles, Practices, Design and Applications (Wiley, 2006).
-
- Kubby J, Gigan S & Cui M Adaptive Optical Microscopy for Biological Imaging (Cambridge Univ. Press, 2019).
Grants and funding
LinkOut - more resources
Full Text Sources
