Observation of the non-linear Meissner effect

Abstract

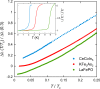
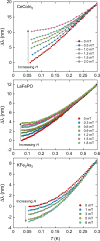
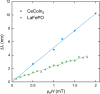
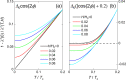
A long-standing theoretical prediction is that in clean, nodal unconventional superconductors the magnetic penetration depth λ, at zero temperature, varies linearly with magnetic field. This non-linear Meissner effect is an equally important manifestation of the nodal state as the well studied linear-in-T dependence of λ, but has never been convincingly experimentally observed. Here we present measurements of the nodal superconductors CeCoIn₅ and LaFePO which clearly show this non-linear Meissner effect. We further show how the effect of a small dc magnetic field on λ(T) can be used to distinguish gap nodes from non-nodal deep gap minima. Our measurements of KFe₂As₂ suggest that this material has such a non-nodal state.

Fig. 1. Temperature dependence of in-plane λ relative to its value at the lowest temperature Δλ(T) for CeCoIn₅, LaFePO, and KFe₂As₂.

For each material, Δλ(T) is normalised by its value at T/T_c = 0.3. The data for CeCoIn₅ and LaFePO have been shifted by ±0.15 along the λ axis for clarity. The inset shows the RF oscillator frequency change over the full temperature range to emphasise the superconducting transitions. Here Δf is measured relative to f(T) just above T_c and normalised to −1 at the lowest temperature. The mid-points of the transition are 2.1, 3.2 and 5.9 K for CeCoIn₅, KFe₂As₂ and LaFePO respectively. For KFe₂As₂ and CeCoIn₅ the RF field is parallel to the ab plane, and for LaFePO the RF field is parallel to the c-axis. Note that these transitions appear broader than the true distribution of T_c in the sample because of the strong T dependence of the normal state skin-depth and the finite sample thickness.

Fig. 2. Effect of magnetic field on the temperature dependence of Δλ.

The finite field data have been shifted along the λ axis to coincide with the zero-field result at T = 0.3 K for CeCoIn₅ and KFe₂As₂ and T = 0.6 K for LaFePO, in order to emphasise the progressive change in the temperature dependence of λ with the field as in Fig. 4.

Fig. 3. Field dependence of Δλ at the lowest temperatures (65 mK) relative to the change at T = 0.3 K (CeCoIn₅) or T = 0.6 K (LaFePO).

The lines are linear fits to the data. Note that no correction for demagnetising effects has been made.

Fig. 4. Calculated temperature dependence of the normalised superfluid density λ²(0)/λ²(T, H).

a d-wave gap structure. b Gap structure is strongly anisotropic but with a small, finite gap. Both cases are in the clean limit and the finite field results have been shifted vertically so that they coincide with the H = 0 results at T/T_c = 0.2 for comparison with our experimental results. Unshifted results and details of the calculations are given in the SI. Note: $1-{\lambda }_0^2/{\lambda }^2\left(T,H\right)\simeq 2\mathrm{\Delta }\lambda \left(T,H\right)/{\lambda }_0$ for small Δλ(T, H).

Fig. 5. Power law exponent analysis for theory and experimental data.

a Evolution of the exponent with field from fits to the theoretical response for different gap structures of the form $\mathrm{\Delta }\left(\varphi ,T\right)={\mathrm{\Delta }}_0\left(T\right)\left(\mid \cos \left(2\varphi \right)\mid +\eta \right)$ and varying impurity concentration Γ (see Supplementary Note 6 for details about the calculations). b–d Experimental response from CeCoIn₅, LaFePO and KFe₂As₂ respectively. The exponent n is extracted from fits to ${\lambda }_0^2/{\left[{\lambda }_0+\mathrm{\Delta }\lambda \left(T\right)\right]}^2=1-A{T}^n$ with upper T limit of 300 mK for CeCoIn₅ and KFe₂As₂, and up to 400 mK for LaFePO. The values assumed for λ₀ were 190 nm for CeCoIn₅, 240 nm for LaFePO and 200 nm for KFe₂As₂. For the fits, to the theoretical response in (a) an upper limit of T/T_c = 0.1 was used. The error bars are the standard error deduced from the fit including a small contribution from the uncertainty in the background determination.