Lossy compression of statistical data using quantum annealer

Abstract

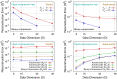
We present a new lossy compression algorithm for statistical floating-point data through a representation learning with binary variables. The algorithm finds a set of basis vectors and their binary coefficients that precisely reconstruct the original data. The optimization for the basis vectors is performed classically, while binary coefficients are retrieved through both simulated and quantum annealing for comparison. A bias correction procedure is also presented to estimate and eliminate the error and bias introduced from the inexact reconstruction of the lossy compression for statistical data analyses. The compression algorithm is demonstrated on two different datasets of lattice quantum chromodynamics simulations. The results obtained using simulated annealing show 3-3.5 times better compression performance than the algorithm based on neural-network autoencoder. Calculations using quantum annealing also show promising results, but performance is limited by the integrated control error of the quantum processing unit, which yields large uncertainties in the biases and coupling parameters. Hardware comparison is further studied between the previous generation D-Wave 2000Q and the current D-Wave Advantage system. Our study shows that the Advantage system is more likely to obtain low-energy solutions for the problems than the 2000Q.

Figure 1

Correlation pattern of the 16 components of the vector (left) and the axial-vector (right) data. Red indicates the high correlation (correlation coefficient = 1), and white indicates no correlation.

Figure 2

$Q^2$, defined in Eq. (8) for different number of storing bits for data dimension $D=16$. For the principal component analysis (PCA) and autoencoder (AE) approaches, the number of storing bits is calculated by $32\times N_z$, assuming single-precision floating-point numbers. For binary compression algorithm of $N_q>=48$, we use the boosting approach with $N_{q1}=N_{q2}=N_q/2$.

Figure 3

Scaling of $Q^2$ for various dimensions (D) vector (left) and axial-vector (right) data. Upper figures show the results using the binary compression algorithm at fixed compression rates ($N_q=D$ and $N_q=2D$), and the bottom figures show the comparison between the binary compression and autoencoder algorithms at fixed sizes in the compressed space ($N_z=1,2,3$ for autoencoder, and $N_q=32$ for binary compression). For binary compression algorithm of $N_q>=48$, we use the boosting approach with $N_{q1}=N_{q2}=N_q/2$.

Figure 4

Cumulative distribution function (CDF) of the normalized reconstruction error from all feasible samples obtained from the D-Wave 2000Q (red) and Advantage system (blue) for the axial-vector data. About 50% and 38% of the samples were feasible from D-Wave 2000Q and Advantage for $N_q=32$, respectively. For $N_q=60$ there were about 51% and 18%, respectively.

Figure 5

Cumulative distribution function (CDF) of the normalized reconstruction error from all feasible samples obtained from the D-Wave 2000Q (red) and Advantage system (blue) for the vector data. About 95% and 91% of the samples were feasible from D-Wave 2000Q and Advantage for $N_q=32$, respectively. For $N_q=60$ there were about 63% and 73%, respectively.