The evolution, evolvability and engineering of gene regulatory DNA
- PMID: 35264797
- PMCID: PMC8934302
- DOI: 10.1038/s41586-022-04506-6
The evolution, evolvability and engineering of gene regulatory DNA
Abstract
Mutations in non-coding regulatory DNA sequences can alter gene expression, organismal phenotype and fitness1-3. Constructing complete fitness landscapes, in which DNA sequences are mapped to fitness, is a long-standing goal in biology, but has remained elusive because it is challenging to generalize reliably to vast sequence spaces4-6. Here we build sequence-to-expression models that capture fitness landscapes and use them to decipher principles of regulatory evolution. Using millions of randomly sampled promoter DNA sequences and their measured expression levels in the yeast Saccharomyces cerevisiae, we learn deep neural network models that generalize with excellent prediction performance, and enable sequence design for expression engineering. Using our models, we study expression divergence under genetic drift and strong-selection weak-mutation regimes to find that regulatory evolution is rapid and subject to diminishing returns epistasis; that conflicting expression objectives in different environments constrain expression adaptation; and that stabilizing selection on gene expression leads to the moderation of regulatory complexity. We present an approach for using such models to detect signatures of selection on expression from natural variation in regulatory sequences and use it to discover an instance of convergent regulatory evolution. We assess mutational robustness, finding that regulatory mutation effect sizes follow a power law, characterize regulatory evolvability, visualize promoter fitness landscapes, discover evolvability archetypes and illustrate the mutational robustness of natural regulatory sequence populations. Our work provides a general framework for designing regulatory sequences and addressing fundamental questions in regulatory evolution.
© 2022. The Author(s), under exclusive licence to Springer Nature Limited.
Conflict of interest statement
Conflict of Interest statement
A.R. is a co-founder and equity holder of Celsius Therapeutics, an equity holder in Immunitas, and until July 31, 2020 was an S.A.B. member of ThermoFisher Scientific, Syros Pharmaceuticals, Neogene Therapeutics and Asimov. From August 1, 2020, A.R. is an employee of Genentech. The other authors declare no competing interests.
Figures






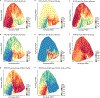
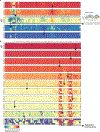

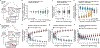

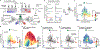
Comment in
-
AI predicts the effectiveness and evolution of gene promoter sequences.Nature. 2022 Mar;603(7901):399-400. doi: 10.1038/d41586-022-00384-0. Nature. 2022. PMID: 35264799 No abstract available.
References
-
- Wittkopp PJ & Kalay G Cis-regulatory elements: molecular mechanisms and evolutionary processes underlying divergence. Nat. Rev. Genet 13, 59–69 (2011). - PubMed
-
- de Visser JAGM & Krug J Empirical fitness landscapes and the predictability of evolution. Nat. Rev. Genet 15, 480–490 (2014). - PubMed
-
- Kondrashov DA & Kondrashov FA Topological features of rugged fitness landscapes in sequence space. Trends in Genetics 31, 24–33 (2015). - PubMed
Methods References
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases
Research Materials

