Cross-linkers at growing microtubule ends generate forces that drive actin transport

Abstract

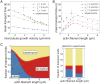
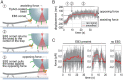
SignificanceComplex cellular processes such as cell migration require coordinated remodeling of both the actin and the microtubule cytoskeleton. The two networks for instance exert forces on each other via active motor proteins. Here we show that, surprisingly, coupling via passive cross-linkers can also result in force generation. We specifically study the transport of actin filaments by growing microtubule ends. We show by cell-free reconstitution experiments, computer simulations, and theoretical modeling that this transport is driven by the affinity of the cross-linker for the chemically distinct microtubule tip region. Our work predicts that growing microtubules could potentially rapidly relocate newly nucleated actin filaments to the leading edge of the cell and thus boost migration.

Keywords: cell biophysics; crosstalk; cytoskeleton; kinetic Monte Carlo simulations; self-organization.

Fig. 1.

Actin transport by growing microtubule plus ends. (A) Schematic depiction of protein domains of ACF7 (Left) and TipAct (Right). CH, calponin homology; GAR, GAS2 related; CC, coiled coil. (B) Schematic of the experimental assay for observing microtubule-mediated actin transport, showing a stabilized actin filament (cyan), the engineered cytolinker TipAct (green-yellow), and the microtubule end-binding protein EB3 (orange) moving freely in solution, while the growing microtubule (red) is anchored to the surface of a functionalized and passivated glass slide. (C) Experimental field of view, showing a typical cropped region that was used for analysis, including microtubules/tubulin (red), EB3 (yellow), TipAct (yellow), and stabilized actin filaments (cyan). (D) Time series of the growing plus end of a microtubule that recruits and transports an actin filament via EB3/TipAct complexes. Arrowheads show the localization of the EB3/TipAct complex (yellow), the binding of a short actin filament (cyan), and the unbinding of this actin filament while the microtubule continues to grow (white). (E) Kymographs (space–time plots) of actin filament transport by the growing plus end of a microtubule, showing the microtubule (red), EB3 and TipAct (yellow), and an actin filament (cyan). From these kymographs, we measure parameters of the microtubule dynamics, such as the growth velocity. (F) Normalized distribution of microtubule growth velocities for growth events where the microtubules do not interact with actin filaments (red) and for microtubules that transport an actin filament (blue). The average growth velocities are 3.5 ± 0.6 µm/min and 3.7 ± 0.7 µm/min for noninteracting and interacting events, respectively. Separate channels are shown in SI Appendix, Fig. S1 C–F. Both EB3 and TipAct are GFP labeled. (Scale bars: 10 µm in C, 5 µm in D, and 5 µm [horizontal] and 60 s [vertical] in E.).

Fig. 2.

Mechanisms limiting the actin transport time. (A) Kymograph of the actin transport event depicted in Fig. 1D, showing that the event ends by the unbinding of the actin filament while the microtubule continues growing for a while (Movie S1). (B) Kymograph of a typical transport event that ends upon a microtubule catastrophe (Movie S2). (C) Kymograph of a typical transport event that ends by loss of contact of the actin filament with the tip, resulting in the actin filament falling behind and lingering on the microtubule (MT) lattice (Movie S3). (D) Kymograph of a typical transport event that ends upon a microtubule catastrophe, but where the shrinking microtubule pulls an actin filament backward (Movie S4). (E) Kymograph of the transport event that ends by the disappearance of the comet at a pausing microtubule. This is the only example of transport ended by microtubule pausing. (F) Distribution of transport distances for actin filaments transported by growing microtubule plus end. Shown are median distance of 2.1 µm (and mean of 2.5 µm) and range of 0.2 to 12.2 µm. (G) Transport distance as a function of actin filament length. Actin filaments that were transported by the growing microtubule plus end have a median length of 1.4 µm (and mean of 1.6 µm) and a length range of 0.5 to 7.9 µm. The maximal length is limited by the tendency of longer filaments to form bundles, which are excluded from further analysis. (H) Categories of termination events together with their observed frequency (n = 265). Typical examples of the categories are shown in A–E. (I) Distributions for the transport times (Top) and microtubule growth velocities (Bottom) are indistinguishable when we consider the complete dataset (n = 265) or the subset of transport events that end by the actin filament unbinding from the microtubule end (i.e., both the “actin unbinds” and “actin falls behind” events, n = 103). Hence, actin unbinding and actin falling behind the tip are statistically independent of microtubule catastrophes (SI Appendix). Separate channels of the kymographs are shown in SI Appendix, Fig. S2. Both TipAct and EB3 are GFP labeled. (Scale bars: 5 µm [horizontal] and 60 s [vertical].).

Fig. 3.

Computer simulations and analytical theory of a mechanism for actin transport by growing MTs. (A) The model used for simulating the interaction between an actin filament (blue, Top) cross-linked to a growing MT (red, Bottom). Both filaments are modeled as one-dimensional inflexible chains of binding sites with lattice constant δ. The MT grows with rate r_g. Cross-linkers are modeled as springs with spring constant k that can be in the solution (state 0), bound to the microtubule only (state 1), or fully connected to both filaments (state 2). These cross-linkers represent a complex of TipAct and EB3, which has a higher affinity for the tip region of the MT (dark red, right) compared to the lattice region (light red, left). The distance between the filaments remains fixed, so the actin filament can only move forward and backward. Viscous interactions with the solution result in a diffusion constant D_a for the actin filament, while the longitudinal components of the pulling forces from the cross-linkers provide additional movement of the actin filament (Movie S5). The cross-linker binding rates from solution to the microtubule lattice and tip regions are $r_{0,1}^{L/T}$, respectively, while the binding rate from a microtubule-bound cross-linker to a fully connected cross-linker is $r_{1,2}$. Each transition is microscopically reversible. (B) A typical time trace of the MT and the actin filament. Compare to Fig. 1D. The actin filament is transported when it interacts with the MT tip region (dark red, front of MT), and can recover from quick detachments from this tip region through diffusion (black arrowhead). However, after a stochastic transport time T_t, the actin filament falls behind the tip region and then performs random diffusion on the MT lattice. (C) Parameter definitions for an analytical theory in a comoving frame. We define x as the position of the front end of the actin filament compared to the back end of the MT tip region. Since the tip region advances upon MT growth, this constitutes a comoving frame of reference. The theory describes the dynamics of x using the cross-linker–induced effective diffusion constant of the actin filament $D_{\text{eff}}\text{}\left(x\right)$, the MT growth velocity v_g, and the effective forward condensation force F_f. The actin filament has a length l_a, the microtubule tip region has a length l_t, and the microtubule lattice region is assumed to extend leftward. The overlap lengths between the actin filament and the microtubule tip and lattice regions are denoted y_t and $y_{\mathcal{l}}$, respectively, and Bottom schematics show the relations between these overlap lengths and the other parameters in three regimes. (D) The effective actin diffusion constant $D_{\text{eff}}\text{}\left(x\right)$ decreases with the overlap between the actin filament and MT lattice region (blue) and the MT tip region (green). Simulations give the proportionality constants of the actin friction coefficients ζ_t and ${\zeta }_{\mathcal{l}}$ by fitting Eq. 1 (lines) to the simulation results (points). (E) Using an analytical expression for the condensation force and the fits from D, the theory predicts a free-energy well (blue line), where a comoving actin position x > 0 within the well represents metastable transport, whereas a barrier crossing at x = 0 and the subsequent slide toward x < 0 represent the actin falling behind the MT tip; the free energy is at a minimum at $x=0.2$ µm where the front of the actin filament is at the front end of the MT tip. Direct sampling of the positional distribution of x in simulations (blue points) confirms the validity of the theoretical prediction. The distance between the two filament ends (top axis) equals $x-l_t$.

Fig. 4.

Comparing experimental, simulation, and theoretical results for the mean transport times. The transport time T_t is defined in Fig. 3B. (A) Mean actin transport time plotted against the growth velocity. Simulations and theoretical predictions are shown for three different actin filament lengths. Experimental data are sorted according to the growth velocity and grouped into four sets with 63 or 64 data points each. The error bars represent $\left({\overline{v}}_{g,i}\pm {\text{SD}}_i,{\overline{T}}_{t,i}\pm {\text{SEM}}_i\right)$, where i labels the four groups, a bar on a random variable represents the sample mean, SD is the SD of the distribution of growth velocities, and the SEM is the SEM of the transport times over that group. The experimental data sample over a distribution of actin lengths ${\overline{l}}_a=1.5\pm 0.8$ µm ($\text{mean}\pm \text{SD}$). The theory correctly predicts both the order of magnitude and the declining trend of the mean transport times. (B) Mean actin transport time plotted against the actin length. Simulations and theoretical predictions are shown for three different microtubule growth velocities. The same experimental data as in A are sorted according to the actin length and divided into four equally sized groups of 63 or 64 data points each, with $v_g=3.8\pm 0.7$ µm min^{– 1} ($\text{mean}\pm \text{SD}$). The experimental data confirm the order of magnitude and the trends of the theoretical predictions. There are insufficient experimental data to test the declining transport times due to increased friction for $l_a>4$ µm and due to increased probability of longer filaments to form bundles; thereby they are excluded from transport analysis. However, for $l_a<4$ µm, the experimental data confirm that the transport time increases due to an increase of the actin binding times when the actin length increases. (C) Fractions of transport events that end by microtubule catastrophes, actin falling behind the microtubule tip region, or actin unbinding from the tip region as a function of actin filament length. The fractions calculated from theoretical values of the catastrophe rate r_c, rate of falling behind r_e, and unbinding rate r_u are plotted as the indicated colored regions. The indicated data points are calculated from in vitro experiments and report the borders between the three transport-termination scenarios as shown in bar plots (Right). Orange indicates border between catastrophe and fall behind; purple indicates border between fall behind and unbind. We group the experimental data into two bins of equal size (discriminated by actin filament length), because the four data bins used in B provide insufficient statistics per bin to calculate two numbers per bin. We calculate the mean actin length (horizontal error bars are the SD) and the fractions at which each mechanism ends the transport events in both bins. We report the borders between these three regions (vertical error bars are the SEM). Microtubule catastrophes lead either to backward actin transport or to actin unbinding, but are always counted as catastrophes in these fractions. The theory overestimates the fraction of events that unbind, but it correctly shows that unbinding events become less important with increasing actin length. The overestimation of the unbinding rate also explains the underestimation of the transport times in A and B.

Fig. 5.

Optical tweezer measurement of the force developed by cargo-bound TipAct at the growing microtubule plus end. (A) Schematic diagram of the experimental setup. A TipAct-coated bead is initially attached to a growing microtubule carrying an EB3 comet: 1) The bead moves back to the center of the trap under the assisting force. 2) After having arrived in the trap center, 3) the bead is pulled by the EB3 comet against the opposing force from the trap. (B) A typical recording of a bead moving against the opposing trap force with experimental steps numbered according to A. The large initial movement of the bead is not caused by an active force from the microtubule, but results from an initially free bead that binds to the microtubule. (C) Examples of forces exerted by growing microtubule ends through the TipAct coupling in presence or absence of EB3. These traces correspond to the complete (untruncated) force traces in SI Appendix, Fig.S9A.