Effects of void nodes on epidemic spreads in networks
- PMID: 35273312
- PMCID: PMC8913681
- DOI: 10.1038/s41598-022-07985-9
Effects of void nodes on epidemic spreads in networks
Abstract
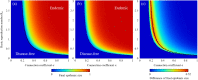
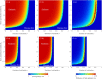
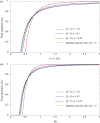
We present the pair approximation models for susceptible-infected-recovered (SIR) epidemic dynamics in a sparse network based on a regular network. Two processes are considered, namely, a Markovian process with a constant recovery rate and a non-Markovian process with a fixed recovery time. We derive the implicit analytical expression for the final epidemic size and explicitly show the epidemic threshold in both Markovian and non-Markovian processes. As the connection rate decreases from the original network connection, the epidemic threshold in which epidemic phase transits from disease-free to endemic increases, and the final epidemic size decreases. Additionally, for comparison with sparse and heterogeneous networks, the pair approximation models were applied to a heterogeneous network with a degree distribution. The obtained phase diagram reveals that, upon increasing the degree of the original random regular networks and decreasing the effective connections by introducing void nodes accordingly, the final epidemic size of the sparse network is close to that of the random network with average degree of 4. Thus, introducing the void nodes in the network leads to more heterogeneous network and reduces the final epidemic size.
© 2022. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures
Similar articles
-
A stochastic SIR network epidemic model with preventive dropping of edges.J Math Biol. 2019 May;78(6):1875-1951. doi: 10.1007/s00285-019-01329-4. Epub 2019 Mar 13. J Math Biol. 2019. PMID: 30868213 Free PMC article.
-
Generalised probability mass function for the final epidemic size of an SIR model on a line of triangles network.Math Biosci. 2019 May;311:49-61. doi: 10.1016/j.mbs.2019.02.003. Epub 2019 Mar 4. Math Biosci. 2019. PMID: 30844380
-
Large epidemic thresholds emerge in heterogeneous networks of heterogeneous nodes.Sci Rep. 2015 Aug 21;5:13122. doi: 10.1038/srep13122. Sci Rep. 2015. PMID: 26293740 Free PMC article.
-
Exact and approximate moment closures for non-Markovian network epidemics.J Theor Biol. 2015 Oct 7;382:160-77. doi: 10.1016/j.jtbi.2015.04.039. Epub 2015 May 12. J Theor Biol. 2015. PMID: 25975999
-
Nodal infection in Markovian susceptible-infected-susceptible and susceptible-infected-removed epidemics on networks are non-negatively correlated.Phys Rev E Stat Nonlin Soft Matter Phys. 2014 May;89(5):052802. doi: 10.1103/PhysRevE.89.052802. Epub 2014 May 1. Phys Rev E Stat Nonlin Soft Matter Phys. 2014. PMID: 25353839
Cited by
-
Scale-free dynamics of COVID-19 in a Brazilian city.Appl Math Model. 2023 Sep;121:166-184. doi: 10.1016/j.apm.2023.03.039. Epub 2023 Apr 21. Appl Math Model. 2023. PMID: 37151217 Free PMC article.
-
Assessing the impact of disease incidence and immunization on the resilience of complex networks during epidemics.Infect Dis Model. 2024 Sep 12;10(1):1-27. doi: 10.1016/j.idm.2024.08.006. eCollection 2025 Mar. Infect Dis Model. 2024. PMID: 39319286 Free PMC article.
-
CONNECTING MASS-ACTION MODELS AND NETWORK MODELS FOR INFECTIOUS DISEASES.ArXiv [Preprint]. 2024 Aug 27:arXiv:2408.15353v1. ArXiv. 2024. PMID: 39253632 Free PMC article. Preprint.
References
-
- Kabir KA, Tanimoto J. Analysis of individual strategies for artificial and natural immunity with imperfectness and durability of protection. J. Theor. Biol. 2021;509:110531. - PubMed
-
- Arefin MR, Masaki T, Tanimoto J. Vaccinating behaviour guided by imitation and aspiration. Proc. R. Soc. A. 2020;476(2239):20200327.
-
- Arefin MR, Kabir KA, Tanimoto J. A mean-field vaccination game scheme to analyze the effect of a single vaccination strategy on a two-strain epidemic spreading. J. Stat. Mech. Theory Exp. 2020;2020(3):033501.
-
- Kabir KA, Kuga K, Tanimoto J. The impact of information spreading on epidemic vaccination game dynamics in a heterogeneous complex network-a theoretical approach. Chaos Solitons Fractals. 2020;132:109548.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical
Research Materials

