Computational models for studying physical instabilities in high concentration biotherapeutic formulations

Abstract

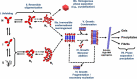
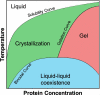
Computational prediction of the behavior of concentrated protein solutions is particularly advantageous in early development stages of biotherapeutics when material availability is limited and a large set of formulation conditions needs to be explored. This review provides an overview of the different computational paradigms that have been successfully used in modeling undesirable physical behaviors of protein solutions with a particular emphasis on high-concentration drug formulations. This includes models ranging from all-atom simulations, coarse-grained representations to macro-scale mathematical descriptions used to study physical instability phenomena of protein solutions such as aggregation, elevated viscosity, and phase separation. These models are compared and summarized in the context of the physical processes and their underlying assumptions and limitations. A detailed analysis is also given for identifying protein interaction processes that are explicitly or implicitly considered in the different modeling approaches and particularly their relations to various formulation parameters. Lastly, many of the shortcomings of existing computational models are discussed, providing perspectives and possible directions toward an efficient computational framework for designing effective protein formulations.

Keywords: Biotherapeutics; aggregation; drug formulation; high concentration; molecular modeling; phase separation; physical instabilities; viscosity.

Figure 1.

Representation of the hierarchy of computational protein models based on their level of resolution, using an IgG2 mAb (PDB: 1IGT) as an example. These types of models include: atomistic; high-resolution coarse-grain (based on the model from Bereau and Deserno); low resolution coarse-grain from Blanco et al.; simplified coarse-grain using the 12-bead model from Calero-Rubio et al. and the 4- and 7-bead models from Blanco et al.; and a continuum model based on Wertheim’s theory adapted by Skar-Gislinge et al. The arrow indicates the direction in which the resolution-level increases for each model.

Figure 2.

Schematic representation of the generalized protein aggregation mechanism for multidomain proteins such as mAbs. The stages shown in the diagram correspond to either effectively reversible steps (double arrows) or irreversible steps (single arrows). Protein oligomerization can occur through self-association of the native monomer (N) or a (partially) unfolded reactive species R. The mechanism also considers the case that N self-associates to a critical size (N_X) to nucleate a homogeneous phase separation (e.g., liquid-liquid separation or crystallization).

Figure 3.

Generic phase diagram for globular proteins adapted from Muschol and Rosenberger. The regions below the solubility curve (i.e., the gel and liquid-liquid coexistence regions) are metastable with respect to crystallization. The liquid-liquid coexistence region, bounded by the binodal curve, corresponds to the thermodynamic state where the solution separates into protein-rich and protein-poor phases. The gelation curve indicates the boundary for the formation of an arrested state. For any protein, the relative position between the solubility, binodal and gelation curves depends on both the protein sequence and solution conditions. Redrawn from Ref. 166.

Figure 4.

Illustrative example of protein-excipient interactions for the variable region of a mAb as calculated by the preferential interaction parameter (${\mathrm{\Gamma }}_{23}$). Panels show the interactions of the antibody with different excipients: (a) Proline; (b) arginine-HCl; and (c) NaCl. Coloring indicates local values of ${\mathrm{\Gamma }}_{23}$, where red indicates preferential inclusion (i.e., attractive interactions). Notably, for all excipients, multiple regions of preferential inclusion are identified along the protein surface. Figure adapted from Cloutier et al.