NMR methods for exploring 'dark' states in ligand binding and protein-protein interactions

Abstract

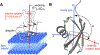
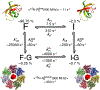
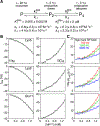
A survey, primarily based on work in the authors' laboratory during the last 10 years, is provided of recent developments in NMR studies of exchange processes involving protein-ligand and protein-protein interactions. We start with a brief overview of the theoretical background of Dark state Exchange Saturation Transfer (DEST) and lifetime line-broadening (ΔR₂) NMR methodology. Some limitations of the DEST/ΔR₂ methodology in applications to molecular systems with intermediate molecular weights are discussed, along with the means of overcoming these limitations with the help of closely related exchange NMR techniques, such as the measurements of Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion, exchange-induced chemical shifts or rapidly-relaxing components of relaxation decays. Some theoretical underpinnings of the quantitative description of global dynamics of proteins on the surface of very high molecular weight particles (nanoparticles) are discussed. Subsequently, several applications of DEST/ΔR₂ methodology are described from a methodological perspective with an emphasis on providing examples of how kinetic and relaxation parameters for exchanging systems can be reliably extracted from NMR data for each particular model of exchange. Among exchanging systems that are not associated with high molecular weight species, we describe several exchange NMR-based studies that focus on kinetic modelling of transient pre-nucleation oligomerization of huntingtin peptides that precedes aggregation and fibril formation.

Keywords: Dark state exchange saturation transfer (DEST); Exchange-induced chemical shifts; Fast component of relaxation decay; Lifetime line-broadening; Relaxation dispersion.

Figure 1.

Modelling of the global dynamics of the protein ubiquitin on the surface of liposome particles. Ubiquitin was chosen as its interaction with liposomes is weak, thereby permitting information in the liposome-bound bound state to be rapidly transferred to the readily observable free state. (A) Ubiquitin (grey ribbon) rotates about an axis (red) perpendicular to the surface of a lipid-based nanoparticle (blue) and wobbles in a cone of semi-angle β₀. (B) The relationship between the internal rotation axis (red) and the axes of the protein inertia tensor (blue) is described by two polar angles: θ, the angle between the internal rotation axis and the z axis of the inertia tensor; and φ, the angle between the x axis and the projection of the internal rotation axis on the x-y plane of the inertia tensor. Adapted from Ceccon et al. [15] published in J. Am. Chem. Soc. (American Chemical Society) while the authors were U.S. Government employees at the National Institutes of Health.

Figure 2.

(A) Plot of ${}^1\text{H}-{\Gamma }_2^{\text{app}}$ versus ${}^1\text{H}-{\Gamma }_2^{\text{calc}}$ calculated using the parameters of exchange between a free protein and a protein in complex with large unilamellar lipid vesicles (LUVs) (k₁ = 50 s⁻¹; k₋₁ = 51,000 s⁻¹; $R_2^{\text{A}}=10{\text{s}}^{-1}$;$R_2^{\text{B}}=13,500{\text{s}}^{-1}$). The asymptotic limit calculated using Eq. (20) is shown with the dashed red line. The inset shows the same plot calculated for the interaction between a protein and small unilamellar lipid vesicles (SUVs) (k₁ = 225 s⁻¹; k₋₁ = 51,000 s⁻¹; $R_2^{\text{A}}=10{\text{s}}^{-1}$; $R_2^{\text{B}}=1,500{\text{s}}^{-1}$). (B) Plot of the ratio of methyl ¹H to methyl ${}^{13}\text{C}{\Gamma }_2^{\text{app}}$ versus ¹H-Γ₂ in the bound state. The region of the plot for ¹H-Γ₂ ≤ 10⁵ s⁻¹ is zoomed in the inset. Adapted from Ceccon et al. [16] published in J. Biomol. NMR while the authors were U.S. Government employees at the National Institutes of Health.

Figure 3.

Examples of ¹⁵N-DEST profiles of (A) Glu3 in the 50 μM Aβ40 sample (¹⁵N-ω₁ = 170 Hz); (B-D) Glu3, Leu17 and Asn27 in the 270 μM Aβ40 sample obtained with ¹⁵N-ω₁ = 170 Hz (orange circles) and 350 Hz (blue circles). The solid line in A is the calculated ¹⁵N-DEST profile with the experimentally determined relaxation rates for monomeric Aβ40. The dashed and solid lines in (B)-(D) are the best fits to a two-state exchange model with a single protofibril-bound state, and to a model incorporating residues tethered and in direct contact with the protofibril (see Fig. 4), respectively. (E) Observed (black filled-in circles) versus calculated ΔR₂ values for the two-state model (grey circles) and the tethered/direct-contact model in Fig. 4 (blue circles). Adapted from Fawzi et al. [2] published in Nature while the authors were U.S. Government employees at the National Institutes of Health.

Figure 4.

Kinetic scheme for residue-specific monomer exchange on the surface of Aβ protofibrils. Circles represent a single residue of Aβ that can exist in three possible chain configurations: (1) a monomer, (2) tethered to, or (3) in direct contact with Aβ protofibrils. Adapted from Fawzi et al. [2] published in Nature while the authors were U.S. Government employees at the National Institutes of Health.

Figure 5.

Kinetics of Aβ40 binding to GroEL. (A) Two-state exchange model describing the association of Aβ40 with GroEL. (B) Illustration of the three possible binding configurations of Aβ40 in the cavity of GroEL. Either the central hydrophobic region or the C-terminal hydrophobic region of Aβ40, or both hydrophobic regions are in contact with GroEL. All the three bound configurations inter-convert faster than the rate of exchange between free and GroEL-bound Aβ40. Adapted from Libich et al. [6] published in Proc. Natl. Acad. Sci. U. S. A. while the authors were U.S. Government employees at the National Institutes of Health.

Figure 6.

Four-state exchange model describing the interactions of Fyn-SH3^VPL with apo-GroEL. F and I represent the free folded and intermediate states, respectively, of Fyn-SH3^VPL, while F-G and I-G are the corresponding GroEL-bound states. The values of the rate constants and populations obtained for the ¹⁵N/protonated SH3 samples from the simultaneous fits to the ¹⁵N CPMG relaxation dispersion, DEST, and ΔR₂ data obtained at 10 °C are indicated. Ribbon diagrams of the free F and I states of Fyn-SH3^VPL together with the side chain of Phe⁴ are shown at the top, while the top view of one cylinder of GroEL, shown as a ribbon with the seven subunits indicated by different colors, and a surface representation of the SH3 domain (red) placed in the cavity, are shown at the bottom. Adapted from Libich et al. [7] published in Proc. Natl. Acad. Sci. U. S. A. while the authors were U.S. Government employees at the National Institutes of Health.

Figure 7.

Simulations of ¹⁵N-CPMG profiles for the four-state model in Fig. 6. Each panel shows the same simulations for different values of Δω^F,I assumed to be equal to Δω^F,I-G (i.e., Δω^I,I-G = 0). Black curves show relaxation dispersions calculated for a two-state system with the interconversion rate constants between the F and I states, k_FI and k_IF, set to the experimentally determined values of 7.5 s⁻¹ and 310 s⁻¹, respectively. Red curves show relaxation dispersions calculated using the four-state model with parameters shown in Fig. 6. Blue curves show relaxation dispersions for a four-state model where the F-G and I-G states do not interconvert directly with one another (i.e. $k^{\text{G}}{}_{\text{FI}}=k^{\text{G}}{}_{\text{IF}}=0$), $k_{\text{on}}^{\text{app}}=6,60,600$, and 6000 s⁻¹, and the population of the I-G state, p_I-G, is kept constant by proportionately scaling k_off (i.e. k_off = 20, 200, 2000, and 2 × 10⁴ s⁻¹), and the remaining rate constants and R₂ values are set to the same values as in the red curves. Adapted from Libich et al. [7] published in Proc. Natl. Acad. Sci. U. S. A. while the authors were U.S. Government employees at the National Institutes of Health.

Figure 8.

Kinetic scheme for the interaction of Fyn-SH3^VPLΔ56 with apo-GroEL. The populations of states U_E and U_B, shown in grey, are below the limits of detection and were therefore not included in analysis. The rate constants and populations relate to experimental conditions of 100 μM SH3 domain and 120 μM GroEL (in subunits) at 10 °C. Binding of the dimer F_D to GroEL is assumed to be undetectable because dimerization occludes the GroEL-binding surface. Adapted from Libich et al. [9] published in Biochemistry while the authors were U.S. Government employees at the National Institutes of Health.

Figure 9.

Average $<{}^{15}\text{N}-R_2^{\text{B}}>$ values for Fyn-SH3^VPLΔ56 (red) and Fyn-SH3^WTΔ57 (black) bound to GroEL as a function of the population of the GroEL-bound state, p_B (%). The $<{}^{15}\text{N}-R_2^{\text{B}}>$ values were determined from minimization of the target functions for either Fyn-SH3^VPLΔ56 (red, 900 MHz) or Fyn-SH3^WTΔ57 (black, 800 MHz) at fixed values of the population of SH3 bound to GroEL (p_B). The regions highlighted in grey denote the ranges of p_B that correspond to realistic $<{}^{15}\text{N}-R_2^{\text{B}}>$ values for the SH3-GroEL complexes at 10°C. Adapted from Libich et al. [9] published in Biochemistry while the authors were U.S. Government employees at the National Institutes of Health.

Figure 10.

Dependence of ¹⁵N-ΔR₂ on the angle γ (deg.) in the presence of (A) LUVs and (B) SUVs. The experimental ¹⁵N-ΔR₂ data are shown as blue circles, and the best-fit curves obtained from a global fit to all the LUV and SUV experimental ΔR₂ data are shown in red (obtained with S_w² = 0.5 and τ_w = 300 ns in Eq. (13)). Adapted from Ceccon et al. [15] published in J. Am. Chem. Soc. (American Chemical Society) while the authors were U.S. Government employees at the National Institutes of Health.

Figure 11.

Experimental ${}^1{\text{H}}_{\text{m}}-{\Gamma }_2^{\text{app}}$ and ${}^{13}{\text{C}}_{\text{m}}-{\Gamma }_2^{\text{app}}$ values measured for methyl groups in ubiquitin in the presence of Gd³⁺-tagged negatively charged POPG (A) LUV liposomes (filled red circles; 1:2 ubiquitin:lipid molar ratio) and (B) SUV liposomes (filled blue circles; 1:0.5 ubiquitin:lipid molar ratio). The dashed horizontal lines in panels A and B show the approximate level of the PRE background. Control PRE values obtained for methyls of ubiquitin with zwitterionic POPC liposomes are shown with open red and blue circles for LUV and SUV particles, respectively, and yield PREs that are essentially all in the background, indicating that the interaction of ubiquitin with negatively charged liposomes is specific and requires a positively charged patch on the surface of ubiquitin. The regions in proximity to ubiquitin-liposome binding interface are highlighted in grey. (C) Experimental ratios of ¹H and ¹³C PREs, $R=\left({}^1{\text{H}}_{\text{m}}-{\Gamma }_2^{\text{app}}\right)/\left({}^{13}{\text{C}}_{\text{m}}-{\Gamma }_2^{\text{app}}\right)$ obtained for ubiquitin in the presence of negatively charged POPG LUV (filled red circles) and SUV (filled blue circles) nanoparticles. As controls, the values of R obtained for ubiquitin in the presence of zwitterionic POPC liposomes are shown with open red circles, and those for GB1 (which does not bind to liposomes) in the presence of negatively charged POPG liposomes are shown with filled black circles. The theoretical ratio of (γ_H/γ_C)² = 16 predicted in the absence of binding is displayed by the horizontal dashed line. Adapted from Ceccon et al. [16] published in J. Biomol. NMR while the authors were U.S. Government employees at the National Institutes of Health.

Figure 12.

Dependence of ¹⁵N-ΔR₂ values on the angle γ for mono- (Ub₁) and di- (Ub₂) ubiquitin. Plots of ¹⁵N-ΔR₂ versus γ for (A) mono-ubiquitin (Ub₁); and the distal (left) and proximal (right) domains of (B) K63- and (C) K48-linked di-ubiquitin Ub₂ (700 MHz). The experimental data points are shown as filled-in and open circles for LUVs and SUVs, respectively. The best-fit curves from the combined analysis of the LUV and SUV data using the spectral density function in Eq. 13, are shown with black lines. In the inset cartoons, the ¹⁵N-labeled domains of Ub₂ are depicted as filled-in circles with the distal and proximal domains of Ub₂ in red and blue, respectively. (D) Schematic representation of the three potential binding modes of Ub₂ to lipid-based nanoparticles with the ‘NMR-active’ ([¹⁵N/²H]-labeled) domain shown in green. Adapted from Ceccon et al. [17] published in J. Phys. Chem. Lett. (American Chemical Society) while the authors were U.S. Government employees at the National Institutes of Health.

Figure 13.

(A) Simulated profiles of C_fast as a function of ¹⁵N frequency offset for Lys⁵ of htt^NT (red) and htt^NTQ₇ (blue) in the presence of SUV vesicles. The curves were calculated using a variant of Eq. (16) that accounts for Δω ≠ 0, with the following values for the exchange parameters (the values in parentheses refer to htt^NTQ₇): k_ex = 205 (208) s⁻¹; p_B = 0.07 (0.08); $R_1^{\text{A}}=R_1^{\text{B}}=1.5(1.5){\text{s}}^{-1}$; $R_2^{\text{A}}=2.4(3.6){\text{ s}}^{-1}$; $R_2^{\text{B}}=2,300(2,300){\text{s}}^{-1}$; ω₁ = 2000 Hz; number of spin locks N = 2; and Δω = −211.8 Hz. (B) Experimental ${}^{15}\text{N}-C_{\text{fast}}^{\text{max}}$ profiles measured for htt^NT (red filled-in circles) and htt^NTQ₇ (blue filled circles) in the presence of SUVs. The open circles are the best-fit profiles obtained by including $C_{\text{fast}}^{\text{max}}$ into the target function together with ¹⁵N-DEST and ΔR₂ profiles. (C) Kinetic scheme used for modelling the binding of htt^NT and htt^NTQ₇ to the surface of SUVs. Adapted from Ceccon et al. [18] published in J. Phys. Chem. B (American Chemical Society) while the authors were U.S. Government employees at the National Institutes of Health.

Figure 14.

Examples of (A) ¹⁵N-DEST profiles and (B) ¹⁵N-ΔR₂ as a function of residue, observed for 300 μM ¹⁵N-labeled htt^NT in the presence of 5 g/L TiO₂ nanoparticles in the dark (600 MHz; 10 °C). Circles represent experimental data, and solid lines are best-fits to a three-state exchange model shown in red at the bottom of panel B. The data for Leu3 and the three C-terminal residues of htt^NT required a separate treatment and were fitted to the three-state model shown in grey. This exchange model subsumes initial binding to the TiO₂ particle followed by reversible detachment from its surface (state ${\text{P}}_{\text{T}}^{\text{red}}$, where ‘T’ denotes ‘tethered’). The rate constants k_BT and k_TB (calculated a posteriori as for the binding of htt^NT to SUV liposomes in the model of Fig. 13B–C using Eqs. (21)), fall in the ranges 40 to 75 s⁻¹ and 160 to 240 s⁻¹, respectively, depending on the assumed red population of the diffusion-restricted state, ${\text{P}}_{\text{R}}^{\text{red}}$. Reversible detachment of these 4 residues from the nanoparticle surface occurs ~3-fold slower than the binding proper (${\text{P}}_{\text{R}}^{\text{red}}\leftrightarrow {\text{P}}_{\text{B}}^{\text{red}}$). Adapted from Ceccon et al. [21] published in J. Am. Chem. Soc. (American Chemical Society) while the authors were U.S. Government employees at the National Institutes of Health.

Figure 15.

Overall kinetic scheme for the binding htt^NT to TiO₂ nanoparticles coupled with oxidation of htt^NT to the Met⁷ sulfoxide form by H₂O₂ either in solution or on the surface of the nanoparticles. States in contact with TiO₂ particles are shaded. Adapted from Ceccon et al. [21] published in J. Am. Chem. Soc. (American Chemical Society) while the authors were U.S. Government employees at the National Institutes of Health.

Figure 16.

Representative concentration-dependent (A) ¹³Cα CPMG relaxation dispersion profiles (900 and 600 MHz), and (B) ¹³Cα δ_ex values (800 MHz) for htt^NTQ₇ (5 °C). The experimental data are shown as open circles. The best-fit curves from a global fit to the kinetic model shown in Fig. 18 are represented by continuous lines. Adapted from Kotler et al. [30] published in Proc. Natl. Acad. Sci. U. S. A. while the authors were U.S. Government employees at the National Institutes of Health.

Figure 17.

Representative (A) ¹⁵N-CPMG relaxation dispersion profiles obtained at 900 and 600 MHz at three concentrations of htt^NTQ₇ (1.0, 0.75, and 0.4 mM; 5 °C), (B) ¹⁵N-R_1ρ relaxation dispersion profiles obtained at 800 and 600 MHz at a concentration of 1.0 mM, and (C) ¹⁵N-δ_ex and ${}^{15}\text{N}-R_2^{1\text{kHz}}$ as a function of htt^NTQ₇ concentration (800 MHz; 5 °C). The experimental data are shown as open circles. The best-fit curves from a global fit to the kinetic model shown in Fig. 18 are represented by continuous lines. Adapted from Kotler et al. [30] published in Proc. Natl. Acad. Sci. U. S. A. while the authors were U.S. Government employees at the National Institutes of Health.

Figure 18.

(A) Kinetic model used to fit all the concentration-dependent NMR data for htt^NTQ₇. The population of the various species at [htt^NTQ₇] = 1.2 mM, the highest concentration used in NMR experiments, is provided in parentheses above each species. (B) Simulation of the population of each species (in monomer units) as a function of total peptide concentration using the rate constants determined from the global fit. The inset shows an expanded view of the dependence over the concentration range used in NMR experiments (0.05 to 1.2 mM). Adapted from Kotler et al. [30] published in Proc. Natl. Acad. Sci. U. S. A. while the authors were U.S. Government employees at the National Institutes of Health.

Figure 19.

Kinetic scheme for oligomerization of the full-length exon-1 peptide, htt^ex1Q₇ containing a seven residue polyglutamine repeat. (A) The ‘on-pathway’ fast branch (τ_ex = 1/k_ex < 50 μs) leading to the formation of the tetramer P₄ via the dimer P₂ is shown in black, while the slow ‘off-pathway’ process (τ_ex ~ 750 μs) leading to the formation of the ‘non-productive’ dimer, ${\text{P}}_2^{*}$, is shown in grey. The fractional populations of each species indicated above the scheme correspond to [htt^ex1] = 1.2 mM. Simulated (B) ¹⁵N-δ_ex and (C) ¹⁵N-R_2,eff relaxation rates for the ‘off-pathway’ (grey) and ‘on-pathway’ (red) branches and the full 4-state scheme of htt^ex1 oligomerization (black) as a function of htt^ex1 concentration. ¹⁵N-R_2,eff values were obtained from on-resonance R_1ρ rates calculated for a spin-lock RF field strength of 1 kHz. Dashed horizontal lines are drawn at zero for comparison. ¹⁵N-Δω was set to −1.1 and −3.1 ppm for the ‘off-pathway’ dimer and the ‘on-pathway’ dimer P₂ and tetramer P₄ (assumed the same), respectively, and ¹⁵N-R₂ was set to 5.0 s⁻¹, while the R₂ of P₂ and P₄ were assumed to scale as 2R₂ and 4R₂, respectively. Adapted from Ceccon et al. [76] published in J. Phys. Chem. Lett. (American Chemical Society) while the authors were U.S. Government employees at the National Institutes of Health.

Figure 20.

(A) Simplified kinetic model of ‘on-pathway’ oligomerization of htt^ex1. The populations of each species indicated above the scheme correspond to those at [htt^ex1] = 1.2 mM. Examples of (B) ¹⁵N/¹³C_α-δ_ex and (C) ¹⁵N-R_2,eff values obtained over the range of htt^ex1 concentrations between 0.1 and 1.4 mM (800 MHz, 5 °C). ¹⁵N-R_2,eff values obtained at RF spin-lock field strengths of 0.75, 1.5 and 3.0 kHz are shown in red, green and blue, respectively. The experimental data are shown as circles; the continuous lines represent the best global fit to the kinetic model shown in (A). Adapted from Ceccon et al. [76] published in J. Phys. Chem. Lett. (American Chemical Society) while the authors were U.S. Government employees at the National Institutes of Health.

Figure 21.

(A) Scheme for the binding of profilin to the two polyproline tracts, P₁₁ and P₁₀, of htt^ex1Q₇. (B) Simulation of the populations of each species during the course of the titrations in each direction, using the best-fit parameters for the equilibrium dissociation constants and cooperativity factor α. Adapted from Ceccon et al. [32] published in Proc. Natl. Acad. Sci. U. S. A. while the authors were U.S. Government employees at the National Institutes of Health.

Figure 22.

(A) Concentration dependence of ¹⁵N- (top, blue circles) and ¹³Cα- (bottom, red circles) δ_ex of htt^ex1Q₇ in the presence of 4.8 mM profilin (800 MHz; 5 °C). The ¹⁵N- and ¹³Cα-δ_ex values obtained for htt^ex1Q₇ in the absence of profilin are shown in grey for comparison. The thick black solid lines represent the back-calculated ¹⁵N-(top) and ¹³Cα-(bottom) δ_ex for ¹⁵N and ¹³Cα Δω values of 2 and 3 ppm, respectively. (B) Examples of ¹⁵N-CPMG relaxation dispersion profiles acquired at 600 (filled-in circles) and 800 (open circles) MHz on 0.4 (green) and 0.75 (blue) mM ¹⁵N-labeled htt^ex1Q₇ in the presence of 4.8 mM profilin. The solid lines are the best-fit curves obtained from global fitting of the ¹⁵N-CPMG relaxation dispersion data to the two-state exchange system shown in black in panel C. (C) Overall kinetic scheme for the oligomerization of htt^ex1Q₇-bound to profilin. The populations of the species correspond to [htt^ex1Q₇] = 0.75 mM. Adapted from Ceccon et al. [32] published in Proc. Natl. Acad. Sci. U. S. A. while the authors were U.S. Government employees at the National Institutes of Health.

Figure 23.

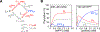
Binding scheme for Fyn-SH3-htt^ex1Q₇ interactions viewed from the perspective of (A) htt^ex1Q₇ and (B) Fyn-SH3. The bold font denotes the magnetization of the isotopically labeled species. Δω_i are the differences in chemical shifts with respect to the major NMR observable state: either monomeric htt^ex1Q₇ (P) or free Fyn-SH3 (L). k_i and k₋₁ are second order association and first order dissociation rate constants, respectively. The species populations, shown in parentheses in (A), relate to [htt^ex1Q₇] = 0.1 mM in the presence of 0.3 mM FynSH3. The equilibrium dissociation constants (mM), expressed in terms of the rate constants, are given by: K_D1 = k₋₁/k₁; K_D2 = k₋₂/2k₂; K_D3 = 2k₋₃/k₃; K_D4 = k₋₄/k₄; and K_D1K_D3 = K_D2K_D4. The optimized values of rate constants are: k₁ = k₃ = 6.4 (±0.7) × 10⁷ M⁻¹s⁻¹, k₂ = k₄ = 4.5 (±0.5) × 10⁶ M⁻¹s⁻¹; k₋₁ = 1.6 (±0.3) × 10⁴ s⁻¹, k₋₂ = 2.9 (±0.3) × 10⁴ s⁻¹, k₋₃ = 7.2 (±1.9) × 10³ s⁻¹, and k₋₄ = 1.4 (±0.5) × 10⁴ s⁻¹, while the derived equilibrium dissociation constants are: K_D1 = 0.25 ± 0.05 mM, K_D2 = 3.3 ± 1.0 mM, K_D3 = 0.30 ± 0.03 mM, and K_D4 = 3.0 ± 0.7 mM. See text for further explanation. Adapted from Ceccon et al. [33] published in J. Am. Chem. Soc. (American Chemical Society) while the authors were U.S. Government employees at the National Institutes of Health.

Figure 24.

Selected examples of ¹⁵N and ¹³Cα CEST profiles for native (A and B) and (Met⁷O) (C and D) htt^NTQ₇ in the presence of micelles (700 MHz; 10 °C). CEST profiles were recorded with ω₁ field strengths of 5 (green), 15 (red) and 25 (blue) Hz. The experimental data are shown as circles and the best-fit profiles for a two-state exchange model as continuous lines. Adapted from Ceccon et al. [31] published in J. Am. Chem. Soc. (American Chemical Society) while the authors were U.S. Government employees at the National Institutes of Health.

Figure 25.

(A) Three-state model for the binding of htt^NTQ_n to lipid micelles that involves dimerization of htt^NTQ_n on the micelle surface. The overall bound state, P_B (shown in green), comprises an equilibrium mixture of monomeric (${\text{P}}_{\text{B}}^{\text{mon}}$) and dimeric (${\text{P}}_{\text{B}}^{\text{dim}}$) states. (B) Average number of monomer and dimer particles bound per micelle calculated using the optimized values of K_D and K_eq. Adapted from Ceccon et al. [31] published in J. Am. Chem. Soc. (American Chemical Society) while the authors were U.S. Government employees at the National Institutes of Health.