Metastable dynamics of neural circuits and networks

Abstract

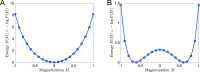
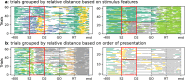
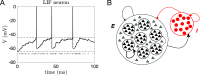
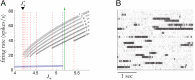
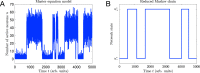
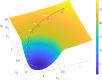
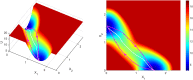
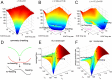
Cortical neurons emit seemingly erratic trains of action potentials or "spikes," and neural network dynamics emerge from the coordinated spiking activity within neural circuits. These rich dynamics manifest themselves in a variety of patterns, which emerge spontaneously or in response to incoming activity produced by sensory inputs. In this Review, we focus on neural dynamics that is best understood as a sequence of repeated activations of a number of discrete hidden states. These transiently occupied states are termed "metastable" and have been linked to important sensory and cognitive functions. In the rodent gustatory cortex, for instance, metastable dynamics have been associated with stimulus coding, with states of expectation, and with decision making. In frontal, parietal, and motor areas of macaques, metastable activity has been related to behavioral performance, choice behavior, task difficulty, and attention. In this article, we review the experimental evidence for neural metastable dynamics together with theoretical approaches to the study of metastable activity in neural circuits. These approaches include (i) a theoretical framework based on non-equilibrium statistical physics for network dynamics; (ii) statistical approaches to extract information about metastable states from a variety of neural signals; and (iii) recent neural network approaches, informed by experimental results, to model the emergence of metastable dynamics. By discussing these topics, we aim to provide a cohesive view of how transitions between different states of activity may provide the neural underpinnings for essential functions such as perception, memory, expectation, or decision making, and more generally, how the study of metastable neural activity may advance our understanding of neural circuit function in health and disease.

FIG. 1.

Example of metastable neural dynamics. (a) Top panel: segmentation of neural activity from nine simultaneously recorded neurons in the rat gustatory cortex. Each line is a spike train, i.e., a sequence of spike times from one of the nine neurons. Recordings were taken as the animal waited and then received a tastant in its mouth at random times (“stimulus”). Colored areas correspond to hidden states of the neural activity, each color representing a different state. A bin of data was assigned to a state if the probability of being in that state, given the data, was higher than 0.8 (colored lines). Bottom panel: the hidden states can be represented as vectors of firing rates across the nine neurons. (b) Same as (a) for “ongoing” neural activity, i.e., for neural activity in the “idle time” between two stimuli. See Sec. V A 8 for details.

FIG. 2.

Energy landscape in an Ising model of N = 20 spins for $T>T_c$ (a) and $T<T_c$ (b). At high temperatures [panel (a)], there is a single minimum at M = 0 and the mean magnetization is $⟨M⟩=0$. At low temperatures [panel (b)], there are two equally probable magnetizations at $M=\pm M_{\text{sp}}$. Thermal fluctuations will cause the magnet to reverse orientation occasionally, such that over time the average magnetization is $⟨M⟩=0$ for any finite N.

FIG. 3.

Sequences of hidden states for the monkey experiment reported in Ref. . Each line is a trial, and each colored segment is a hidden state. White segments correspond to epochs in which no hidden state could be assigned with the necessary confidence. (a) This panel shows hidden states that are coding states for relative distance based on stimulus features, occurring during the presentation of the second stimulus (“S2,” red box). By definition, these hidden states were statistically more often present depending on whether the further stimulus from the center was a blue circle (bottom trials) or a red square (top trials). Two example sessions are shown; coding states are the dark green and yellow states in the left panel and the dark green and gray states in the right panel. (b) Coding states for relative distance based on the order of presentation during the second stimulus (two example sessions shown). Coding states are the dark green, orange, and gray states in the left panel and the yellow state in the right panel. In this case, the coding states were more often present if further stimulus appeared first (bottom trials) or last (top trials). In both panels, trials were grouped according to the coded variable and highlighted by the red box. The same colors in different panels do not imply the same state. Reproduced with permission from D. Benozzo et al., Cell Rep. 35, 108934 (2021). Copyright 2021 Author(s), licensed under a Creative Commons Attribution 4.0 License.

FIG. 4.

Inferring metastable dynamics from spike train observations can only recover the theoretical phase portrait. The spike trains were generated from a winner-take-all decision-making model implemented with spiking neural network. The tree-structured recurrent switching linear dynamical system (TrSLDS) model is fit to subsampled spike trains. Inference was performed using augmented Gibbs-sampling. (a) Overview of the connectivity structure of the spiking neural network. [(b) and (c)] Raster plots of excitatory neurons for two random trials. (d) The latent trajectories converge to either one of the two of sinks at the end of trial (green). Each trajectory is colored by their final choice. [(e)–(g)] Dynamics inferred by each level of the tree structure provide a multi-scale view. The most detailed view in (g) exhibits one saddle (cyan) and two stable fixed points (black). (h) Theoretically reduced two-dimensional phase portrait of the spiking neural network dynamics given the full specification and no data. The green and yellow curves are nullclines. Note the similarity between (g) and (h). Reproduced with permission from J. Nassar et al., 52nd Asilomar Conference on Signals, Systems and Computers (2018). Copyright 2018 Institute of Electrical and Electronics Engineers.

FIG. 5.

(a) Simulation of a leaky integrate-and-fire (LIF) neuron in response to an excitatory Poisson spike train (sequence of tickmarks at the bottom). (b) Schematic diagram of a clustered spiking network. E = excitatory neurons and I = inhibitory neurons. See the text for details.

FIG. 6.

(a) Mean field analysis of the clustered spiking network of Fig. 5(b) with Q = 30 clusters. $J_{+}^{*}$ is the first critical point for the mean synaptic weight inside each cluster; the blue diamonds represent activity configurations with no “active” clusters (i.e., the firing rate in each cluster remains at the level of “spontaneous activity”; see the text for details). (b) Rasterplot of the network in panel (a) for a value of $J_{+}=5.2$ [green vertical line in panel (a)], illustrating metastable dynamics in this network. The network comprises 4000 E neurons and 1000 I neurons; the sequence of dots in each line is a spike train emitted by the neuron represented on that line. Transient activations of clusters of neurons is visible as darker bands (see the text for details). Reproduced with permission from L. Mazzucato et al., J. Neurosci. 35, 8214–8231 (2015). Copyright 2015 the Authors.

FIG. 7.

Simulations of the stochastic dynamics of a single population of active and inactive neurons. (a) Full simulation of the master equation model Eq. (14) with $f_0=2$, γ = 1, $\theta =0.86$, and N = 20 (interpreted as the average number of synaptic inputs each neuron receives). (b) Reduced Markov chain [Eq. (17)] using the estimated escape rates $r_{\pm }$ from each of the fixed point states $u_{+}^{\ast }$ to $u_{-}^{\ast }$ or vice versa. See text for details of the meaning of each parameter. This figure replicates the results shown in Fig. 6 of Ref. , up to stochastic differences in simulations.

FIG. 8.

An illustration of a driving force and flux on the underlying non-equilibrium landscape. x₁ and x₂ are state variables in arbitrary units. White arrows represent the flux, and pink arrows represent the force from the negative gradient of the potential landscape. See the text for details.

FIG. 9.

2D and 3D illustration of non-equilibrium landscape with the irreversible dominant transition paths between basins (purple lines with arrows) and the gradient path (white line). x₁ and x₂ are state variables (arbitrary units). U is the underlying non-equilibrium potential. See the text for details. Reproduced with permission from H. Feng et al., Chem. Sci. 5, 3761–3769 (2014). Copyright 2014 The Royal Society of Chemistry.

FIG. 10.

(a) Schematic diagram of the energy function landscape of the Hopfield network. (b) The potential landscape ${\varphi }_0(\mathit{x})$ of a symmetric neural network. (c) The potential landscape ${\varphi }_0(\mathit{x})$ as well as the corresponding force for an asymmetric neural circuit: the green arrows represent the flux, and the white arrows represent the force from the negative gradient of the potential landscape. Reproduced with permission from H. Yan et al., Proc. Natl. Acad. Sci. U. S. A. 110, E4185–E4194 (2013). Copyright 2013 the Authors.

FIG. 11.

(a) and (b) The schematic diagram of the circuit model for working memory (WM). The model comprises two selective, excitatory populations, labeled 1 and 2. Each excitatory population is recurrently connected and inhibits each other through a common pool of inhibitory interneurons. (c) and (d) The schematic diagrams for the WM during different phases in a WM task. (e)–(h) The corresponding potential landscapes in the (S1; S2) state space during different phases. The dimensionless quantities S1 and S2 are average synaptic gating variables of the two selective populations, which can represent the mean population activities. The label “r” indicates the attractor representing the resting state. The attractors representing the target-related and distractor-related memory state are labeled with “m1” and “m2,” respectively. Reproduced with permission from H. Yan and J. Wang, PLoS Comput. Biol. 16, e1008209 (2020). Copyright 2020 Author(s), licensed under a Creative Commons Attribution (CC BY) license.

FIG. 12.

(a)–(f) The robustness against random fluctuations during the maintenance phase. (a)–(c) The potential landscapes for different self-excitations $J_{+}$. (d) The schematic diagram of the barrier heights on the corresponding potential landscapes for increasing $J_{+}$. (e) and (f) Robustness of WM against random fluctuations as a function of self-excitations $J_{+}$ and mutual inhibition $J_{-}$ through quantifying the corresponding barrier height and the mean first passage time. (g)–(l) The robustness against distractors during the maintenance phase. Reproduced with permission from H. Yan and J. Wang, PLoS Comput. Biol. 16, e1008209 (2020). Copyright 2020 Author(s), licensed under a Creative Commons Attribution (CC BY) license.

FIG. 13.

(a) The schematic diagram of the reduced two population decision-making model. This reduced model consists of two competing neural populations that are selective for leftward or rightward directions, respectively. (b) The schematic representation of the random dots motion. For higher motion coherence, most dots move in one direction, whereas the dots move with no directional bias at a low motion coherence level. (c) The potential landscape of the decision-making network with varying inputs and pathways. The pink lines indicate the paths of decision making from undecided state to decided states. The red dotted lines represent the paths from the two decided states back to the undecided state. (d)–(g) The mechanism of changes of mind based on the emergence of the new intermediate state in the center. (d) and (e) The two-dimensional potential landscapes for different large inputs at the zero coherence level. (f) and (g) The two-dimensional potential landscapes for a large input when the motion coherence $c\prime =0.02$ and 0.06, respectively. Reproduced with permission from H. Yan et al., Chin. Phys. B 25, 078702 (2016). Copyright 2016 Chinese Physical Society and IOP Publishing.

FIG. 14.

(a)–(c) Potential landscapes for different inputs. The increase in the inputs induces symmetry breaking from the symmetric but featureless state to the biased state with biological functions. The fluxes are indicated by purple arrows. λ₁ and λ₂ represent the strength of the inputs to the SOM+ and SOM− neurons, respectively. (d) A diagram of how a one-dimensional potential landscape changes with stimulus inputs. (e) Average flux landscape in the space of different inputs. The average flux is significantly positively correlated with the external inputs, when the neural circuit is away from its equilibrium state. (f) The entropy production rate landscape in the space of different inputs. The neural circuit dissipates more energy with larger inputs. It costs more energy to maintain the dominant freezing responses than dominant no-freezing behaviors. λ₁ and λ₂: same as is panels (a)–(c). Reproduced with permission from H. Yan et al., J. R. Soc. Interface 16, 20180756 (2019). Copyright 2019 The Royal Society.