Strategy-dependent effects of working-memory limitations on human perceptual decision-making
- PMID: 35289747
- PMCID: PMC9005192
- DOI: 10.7554/eLife.73610
Strategy-dependent effects of working-memory limitations on human perceptual decision-making
Abstract
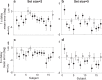
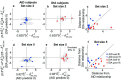
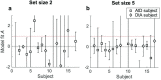
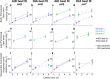
Deliberative decisions based on an accumulation of evidence over time depend on working memory, and working memory has limitations, but how these limitations affect deliberative decision-making is not understood. We used human psychophysics to assess the impact of working-memory limitations on the fidelity of a continuous decision variable. Participants decided the average location of multiple visual targets. This computed, continuous decision variable degraded with time and capacity in a manner that depended critically on the strategy used to form the decision variable. This dependence reflected whether the decision variable was computed either: (1) immediately upon observing the evidence, and thus stored as a single value in memory; or (2) at the time of the report, and thus stored as multiple values in memory. These results provide important constraints on how the brain computes and maintains temporally dynamic decision variables.
Keywords: computational biology; decision making; human; neuroscience; psychophysics; systems biology; working memory.
Plain language summary
Working memory, the brain’s ability to temporarily store and recall information, is a critical part of decision making – but it has its limits. The brain can only store so much information, for so long. Since decisions are not often acted on immediately, information held in working memory ‘degrades’ over time. However, it is unknown whether or not this degradation of information over time affects the accuracy of later decisions. The tactics that people use, knowingly or otherwise, to store information in working memory also remain unclear. Do people store pieces of information such as numbers, objects and particular details? Or do they tend to compute that information, make some preliminary judgement and recall their verdict later? Does the strategy chosen impact people’s decision-making? To investigate, Schapiro et al. devised a series of experiments to test whether the limitations of working memory, and how people store information, affect the accuracy of decisions they make. First, participants were shown an array of colored discs on a screen. Then, either immediately after seeing the disks or a few seconds later, the participants were asked to recall the position of one of the disks they had seen, or the average position of all the disks. This measured how much information degraded for a decision based on multiple items, and how much for a decision based on a single item. From this, the method of information storage used to make a decision could be inferred. Schapiro et al. found that the accuracy of people’s responses worsened over time, whether they remembered the position of each individual disk, or computed their average location before responding. The greater the delay between seeing the disks and reporting their location, the less accurate people’s responses tended to be. Similarly, the more disks a participant saw, the less accurate their response became. This suggests that however people store information, if working memory reaches capacity, decision-making suffers and that, over time, stored information decays. Schapiro et al. also noticed that participants remembered location information in different ways depending on the task and how many disks they were shown at once. This suggests people adopt different strategies to retain information momentarily. In summary, these findings help to explain how people process and store information to make decisions and how the limitations of working memory impact their decision-making ability. A better understanding of how people use working memory to make decisions may also shed light on situations or brain conditions where decision-making is impaired.
© 2022, Schapiro et al.
Conflict of interest statement
KS, KJ, ZK No competing interests declared, JG Senior editor, eLife
Figures




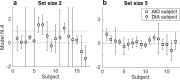
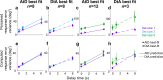
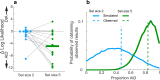
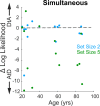




References
Publication types
MeSH terms
Associated data
Grants and funding
LinkOut - more resources
Full Text Sources

