Finger stability in precision grips

Abstract

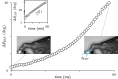
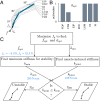
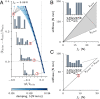
Stable precision grips using the fingertips are a cornerstone of human hand dexterity. However, our fingers become unstable sometimes and snap into a hyperextended posture. This is because multilink mechanisms like our fingers can buckle under tip forces. Suppressing this instability is crucial for hand dexterity, but how the neuromuscular system does so is unknown. Here we show that people rely on the stiffness from muscle contraction for finger stability. We measured buckling time constants of 50 ms or less during maximal force application with the index finger—quicker than feedback latencies—which suggests that muscle-induced stiffness may underlie stability. However, a biomechanical model of the finger predicts that muscle-induced stiffness cannot stabilize at maximal force unless we add springs to stiffen the joints or people reduce their force to enable cocontraction. We tested this prediction in 38 volunteers. Upon adding stiffness, maximal force increased by 34 ± 3%, and muscle electromyography readings were 21 ± 3% higher for the finger flexors (mean ± SE). Muscle recordings and mathematical modeling show that adding stiffness offloads the demand for muscle cocontraction, thus freeing up muscle capacity for fingertip force. Hence, people refrain from applying truly maximal force unless an external stabilizing stiffness allows their muscles to apply higher force without losing stability. But more stiffness is not always better. Stiff fingers would affect the ability to adapt passively to complex object geometries and precisely regulate force. Thus, our results show how hand function arises from neurally tuned muscle stiffness that balances finger stability with compliance.

Keywords: cocontraction; human hand; muscle elasticity; precision grip; stability.

Fig. 1.

Buckling of the index finger joints. Sample trial showing the change in the angle of the DIP, $\mathrm{\Delta }{\theta }_{\text{DIP}}$. Every fifth sample is plotted for clarity (black circles). (Top Inset) Linear log plot of the exponential growth in DIP angle. The time constant τ for the unstable growth in $\mathrm{\Delta }{\theta }_{\text{DIP}}$ is found using the slope. For this trial, τ = 20 ms. (Bottom Insets) Snapshots of the index finger at the beginning and the end of the sample trial.

Fig. 2.

Modeling study to test whether stability is a byproduct of fingertip force. (A) Schematic of a planar model of the index finger that maintains contact at the fingertip and is driven by seven muscles. All seven muscles attach to locations in the hand and arm that are proximal to the MCP joint. (B) The optimal activation pattern ${\overrightarrow{a}}_{\text{opt}}$ that maximizes the vertical component of the fingertip force at a fixed posture $\overrightarrow{\theta }=({30}^{°},{30}^{°},{10}^{°})$. This is the posture used in subsequent experiments in this paper. (C) The decision tree to test whether muscle-induced stiffness leads to stability when the activation pattern is chosen solely to maximize fingertip force. The computed force and stiffnesses at $\overrightarrow{\theta }=({30}^{°},{30}^{°},{10}^{°})$ are in blue. The finger is unstable at the maximal force because $k_{\text{joint}}<k_{\min }$.

Fig. 3.

Maximal force upon stiffening the finger. (A) Three conditions were tested at the posture $({30}^{°},{30}^{°},{10}^{°})$: no splint (free), two-joint split (2J), or one-joint splint (1J). (B) For a sample subject, the shaded rectangles show the time window when the maximal force occurred, pink for 2J and yellow for free, which are overlaid on the vertical force and raw EMG recordings from FDP and FDS. EMG rectangles are scaled 6× for clarity, but the force rectangles are to scale. (C) Change due to the 2J and 1J splints, relative to the free finger, in the maximal normalized force $f_{\max }$, flexor EMG, and extensor EMG. The bars and whiskers show the mean and SE, respectively. (D) Scatter plots and regression fits of the change in EMG versus change in force between the splint and the free conditions, for the 2J and 1J conditions.

Fig. 4.

Cocontraction and maximal force. (A) Ratio of extensor to flexor activity for the free, 1J, and 2J splint conditions (n = 16). For A and C, the bars and whiskers show the mean and SE, respectively. (B) Pictorial demonstration of the hypothesis that the free finger is more cocontracted relative to the splinted condition, as seen by a steeper slope for the free finger compared to the splint condition in the normalized EMG–force space. (C) EMG to normalized force ratios for the flexors FDS and FDP, and the extensor EDC, for the free, 1J, and 2J splint conditions (n = 16). (D) Scatter plot and regression fit of the change in EDC cocontraction versus the change in normalized force. The scatter plot is colored by the magnitude of the free finger’s baseline force (n = 16). (E) Scatter plot and regression fits of the free finger’s baseline force versus the change in force between the splinted and the free conditions for the 2J (black, n = 38) and the 1J (gray, n = 29) splints.

Fig. 5.

Muscle cocontraction, stiffness, and stability at submaximal force. (A) Monte Carlo simulations densely sampled the 4D space of activation patterns, all of which produce the same tip force but vary in stiffness and stability ($f_y=9.1$ N, $f_x=-8.0$ N). Using the nondimensional variables $\eta b/k_{\min }$ and $(k_{\text{joint}}-k_{\min })/k_{\min }$ for stability and stiffness, respectively, the 4D space of activations collapses into a family of 1D curves that are parametrized by the damping value. Near the origin, the 1D stability–stiffness curves merge into a universal line with slope $=-1$ according to the asymptotic relation given in Eq. 3. (B) The unstable optimal activation ${\overrightarrow{a}}_{\text{opt}}$ (Inset) that maximizes tip force, and (C) the marginally stable pattern “2” are linearly scaled to vary the tip force. The joint stiffness $k_{\text{joint}}$ and the minimum stiffness $k_{\min }$ also scale linearly, thus preserving the stability properties of the original activation pattern. (Inset) Maximally scaled up version of pattern “2.” Posture for all plots: $({30}^{°},{30}^{°},{10}^{°})$.