Persistent cell migration emerges from a coupling between protrusion dynamics and polarized trafficking
- PMID: 35302488
- PMCID: PMC8963884
- DOI: 10.7554/eLife.69229
Persistent cell migration emerges from a coupling between protrusion dynamics and polarized trafficking
Abstract
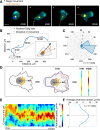
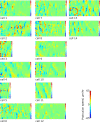
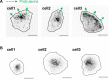
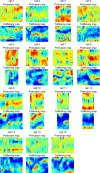
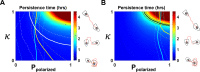
Migrating cells present a variety of paths, from random to highly directional ones. While random movement can be explained by basal intrinsic activity, persistent movement requires stable polarization. Here, we quantitatively address emergence of persistent migration in (hTERT)-immortalizedRPE1 (retinal pigment epithelial) cells over long timescales. By live cell imaging and dynamic micropatterning, we demonstrate that the Nucleus-Golgi axis aligns with direction of migration leading to efficient cell movement. We show that polarized trafficking is directed toward protrusions with a 20-min delay, and that migration becomes random after disrupting internal cell organization. Eventually, we prove that localized optogenetic Cdc42 activation orients the Nucleus-Golgi axis. Our work suggests that polarized trafficking stabilizes the protrusive activity of the cell, while protrusive activity orients this polarity axis, leading to persistent cell migration. Using a minimal physical model, we show that this feedback is sufficient to recapitulate the quantitative properties of cell migration in the timescale of hours.
Keywords: Golgi apparatus; RhoGTPase; cell architecture; cell biology; human; model; optogenetics; persistent migration; physics of living systems; polarity; polarized trafficking; subcellular organization.
© 2022, Vaidžiulytė et al.
Conflict of interest statement
KV, AM, AB, WB, KS, MC No competing interests declared
Figures











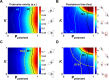

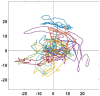
Similar articles
-
The Golgi apparatus and cell polarity: Roles of the cytoskeleton, the Golgi matrix, and Golgi membranes.Curr Opin Cell Biol. 2020 Feb;62:104-113. doi: 10.1016/j.ceb.2019.10.003. Epub 2019 Nov 18. Curr Opin Cell Biol. 2020. PMID: 31751898 Review.
-
Golgi polarity does not correlate with speed or persistence of freely migrating fibroblasts.Eur J Cell Biol. 2009 Dec;88(12):711-7. doi: 10.1016/j.ejcb.2009.08.001. Epub 2009 Sep 2. Eur J Cell Biol. 2009. PMID: 19726103 Free PMC article.
-
Geometric control of cell migration.Sci Rep. 2013 Oct 3;3:2827. doi: 10.1038/srep02827. Sci Rep. 2013. PMID: 24089214 Free PMC article.
-
Subcellular optogenetic activation of Cdc42 controls local and distal signaling to drive immune cell migration.Mol Biol Cell. 2016 May 1;27(9):1442-50. doi: 10.1091/mbc.E15-12-0832. Epub 2016 Mar 3. Mol Biol Cell. 2016. PMID: 26941336 Free PMC article.
-
Microtubules in cell migration.Annu Rev Cell Dev Biol. 2013;29:471-99. doi: 10.1146/annurev-cellbio-101011-155711. Epub 2013 Jul 12. Annu Rev Cell Dev Biol. 2013. PMID: 23875648 Review.
Cited by
-
Time-resolved proximity proteomics uncovers a membrane tension-sensitive caveolin-1 interactome at the rear of migrating cells.Elife. 2024 Sep 24;13:e85601. doi: 10.7554/eLife.85601. Elife. 2024. PMID: 39315773 Free PMC article.
-
Follow the flow: Actin and membrane act as an integrated system to globally coordinate cell shape and movement.Curr Opin Cell Biol. 2024 Aug;89:102392. doi: 10.1016/j.ceb.2024.102392. Epub 2024 Jul 10. Curr Opin Cell Biol. 2024. PMID: 38991476 Free PMC article. Review.
-
Advances in Regulating Cellular Behavior Using Micropatterns.Yale J Biol Med. 2023 Dec 29;96(4):527-547. doi: 10.59249/UXOH1740. eCollection 2023 Dec. Yale J Biol Med. 2023. PMID: 38161579 Free PMC article. Review.
-
Oscillatory ERK Signaling and Morphology Determine Heterogeneity of Breast Cancer Cell Chemotaxis via MEK-ERK and p38-MAPK Signaling Pathways.Bioengineering (Basel). 2023 Feb 18;10(2):269. doi: 10.3390/bioengineering10020269. Bioengineering (Basel). 2023. PMID: 36829763 Free PMC article.
-
MLC2: Physiological Functions and Potential Roles in Tumorigenesis.Cell Biochem Biophys. 2025 Mar 16. doi: 10.1007/s12013-025-01721-6. Online ahead of print. Cell Biochem Biophys. 2025. PMID: 40089610 Review.
References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
Miscellaneous

