A multiscale model of virus pandemic: Heterogeneous interactive entities in a globally connected world
- PMID: 35309741
- PMCID: PMC8932953
- DOI: 10.1142/s0218202520500323
A multiscale model of virus pandemic: Heterogeneous interactive entities in a globally connected world
Abstract
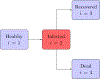
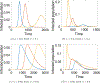
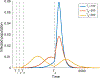
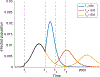
This paper is devoted to the multidisciplinary modelling of a pandemic initiated by an aggressive virus, specifically the so-called SARS-CoV-2 Severe Acute Respiratory Syndrome, corona virus n.2. The study is developed within a multiscale framework accounting for the interaction of different spatial scales, from the small scale of the virus itself and cells, to the large scale of individuals and further up to the collective behaviour of populations. An interdisciplinary vision is developed thanks to the contributions of epidemiologists, immunologists and economists as well as those of mathematical modellers. The first part of the contents is devoted to understanding the complex features of the system and to the design of a modelling rationale. The modelling approach is treated in the second part of the paper by showing both how the virus propagates into infected individuals, successfully and not successfully recovered, and also the spatial patterns, which are subsequently studied by kinetic and lattice models. The third part reports the contribution of research in the fields of virology, epidemiology, immune competition, and economy focussed also on social behaviours. Finally, a critical analysis is proposed looking ahead to research perspectives.
Keywords: 92C60; 92D30; COVID-19; SARS-CoV-2; complexity; immune competition; intracellular infection dynamics; living systems; multiscale problems; networks; spatial patterns; viral quasispecies; virus structure modelling.
Figures

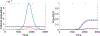
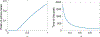
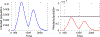
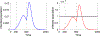
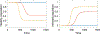
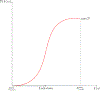
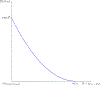
References
-
- Adhikari P, Intra- and intermolecular atomic-scale interaction of the receptor binding domain in SARS-CoV-2 spike protein: Implication for ACE2 receptor binding, preprint (2020). - PubMed
-
- Albi G, Bellomo N, Fermo L, Ha S-Y, Kim J, Pareschi L, Poyato D and Soler J, Traffic, crowds, and swarms. From kinetic theory and multiscale methods to applications and research perspectives, Math. Models Methods Appl. Sci 29 (2019) 1901–2005.
-
- Anderson RA and May RM, Population biology of infectious diseases: Part I, Nature 280 (1979) 361–367. - PubMed
-
- Anderson RA and May RM, Population biology of infectious diseases: Part II, Nature 280 (1979) 455–461. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
