Evaluation of tree-based statistical learning methods for constructing genetic risk scores

Abstract

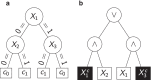
Background: Genetic risk scores (GRS) summarize genetic features such as single nucleotide polymorphisms (SNPs) in a single statistic with respect to a given trait. So far, GRS are typically built using generalized linear models or regularized extensions. However, these linear methods are usually not able to incorporate gene-gene interactions or non-linear SNP-response relationships. Tree-based statistical learning methods such as random forests and logic regression may be an alternative to such regularized-regression-based methods and are investigated in this article. Moreover, we consider modifications of random forests and logic regression for the construction of GRS.

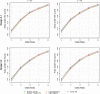
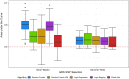
Results: In an extensive simulation study and an application to a real data set from a German cohort study, we show that both tree-based approaches can outperform elastic net when constructing GRS for binary traits. Especially a modification of logic regression called logic bagging could induce comparatively high predictive power as measured by the area under the curve and the statistical power. Even when considering no epistatic interaction effects but only marginal genetic effects, the regularized regression method lead in most cases to inferior results.

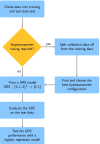
Conclusions: When constructing GRS, we recommend taking random forests and logic bagging into account, in particular, if it can be assumed that possibly unknown epistasis between SNPs is present. To develop the best possible prediction models, extensive joint hyperparameter optimizations should be conducted.

Keywords: Bagging; Elastic net; Epistasis; Logic regression; Polygenic risk scores; Random forests; Simulation study; Statistical learning; Variable selection.

Fig. 1

Workflow of constructing and evaluating genetic risk scores

Fig. 2

Exemplary tree models for three binary input variables $X_1$, $X_2$ and $X_3$ predicting two different classes $c_0$ and $c_1$. In a, a classification tree is shown. b depicts a logic tree describing the Boolean expression $(X_1^c\wedge X_2)\vee (X_1\wedge X_3^c)$. Here, a true Boolean expression is identified as class $c_1$ and $c_0$ otherwise. Negated input variables/leaves are marked by white letters on a black background. Both trees are equivalent, i.e., they perform the same predictions for each predictor setting

Fig. 3

Mean AUC for random forests, random forests VIM, logic regression, logic bagging, elastic net, and the true underlying model in the first simulation scenario considering marginal effective SNPs evaluated on the test data

Fig. 4

Mean AUC for random forests, random forests VIM, logic regression, logic bagging, elastic net, and the true underlying model in the second simulation scenario incorporating interactions of SNPs evaluated on the test data. The Designs 2.1, 2.2, and 2.3 describe the scenarios where both interacting SNPs also exhibit marginal effects, only one of both SNPs shows a marginal signal or none of them induce a main effect, i.e., (j, k) = (1, 2), (1, 4), or (4, 5) in Eq. (3), respectively

Fig. 5

Mean AUC for random forests, random forests VIM, logic regression, logic bagging, and elastic net in the third simulation scenario incorporating continuous input variables evaluated on the test data. The Designs 3.1 and 3.2 describe the scenarios where the GxE interacting SNP also exhibits a moderate marginal effect or where it does not induce a main effect, i.e., j = 2 or 5 in Eq. (4), respectively

Fig. 6

AUC for random forests, random forests VIM, logic regression, logic bagging, and elastic net in the application to data from the SALIA study evaluated on the test data. Results for single unadjusted models also considering the alternative genome-wide construction approach

Fig. 7

AUC for random forests, random forests VIM, logic regression, logic bagging, and elastic net in the application to data from the SALIA study evaluated on the test data. Results for the final age-adjusted models with different air pollution indicators