Analytical Modeling of Flowrate and Its Maxima in Electrochemical Bioelectronics with Drug Delivery Capabilities

Abstract

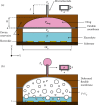
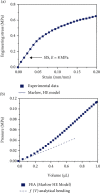
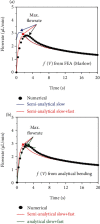
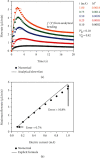
Flowrate control in flexible bioelectronics with targeted drug delivery capabilities is essential to ensure timely and safe delivery. For neuroscience and pharmacogenetics studies in small animals, these flexible bioelectronic systems can be tailored to deliver small drug volumes on a controlled fashion without damaging surrounding tissues from stresses induced by excessively high flowrates. The drug delivery process is realized by an electrochemical reaction that pressurizes the internal bioelectronic chambers to deform a flexible polymer membrane that pumps the drug through a network of microchannels implanted in the small animal. The flowrate temporal profile and global maximum are governed and can be modeled by the ideal gas law. Here, we obtain an analytical solution that groups the relevant mechanical, fluidic, environmental, and electrochemical terms involved in the drug delivery process into a set of three nondimensional parameters. The unique combinations of these three nondimensional parameters (related to the initial pressure, initial gas volume, and microfluidic resistance) can be used to model the flowrate and scale up the flexible bioelectronic design for experiments in medium and large animal models. The analytical solution is divided into (1) a fast variable that controls the maximum flowrate and (2) a slow variable that models the temporal profile. Together, the two variables detail the complete drug delivery process and control using the three nondimensional parameters. Comparison of the analytical model with alternative numerical models shows excellent agreement and validates the analytic modeling approach. These findings serve as a theoretical framework to design and optimize future flexible bioelectronic systems used in biomedical research, or related medical fields, and analytically control the flowrate and its global maximum for successful drug delivery.

Figure 1

Simplified schematic of a bioelectronic layout used for drug delivery. (a) Before the drug delivery process, the electrolyte reservoir is partially filled where an initial volume of gas and the drug sits on top of the flexible membrane. (b) The gas formation process deforms the flexible membrane to pump the drug from inside the device through the microchannels and into the target location. The parameters involved in the drug delivery process are labeled through the schematic in their respective locations except the Young modulus, Poisson ratio, and stress-strain relationship of the flexible membrane.

Figure 2

Mechanics of the flexible membrane. (a) Stress-strain experimental data for a representative SIS polymer selected for the flexible membrane (squares) and the Marlow hyperelastic (HE) model fit of the data (solid line). (b) Pressure-volume relationship for the SIS polymer obtained from FEA using the Marlow HE model (squares) and the pressure-volume relationship derived from plate theory for bending-dominated deformation (dashed line). The flexible membrane dimensions are thickness h = 150 μm and radius R₀ = 1.20 mm.

Figure 3

Flowrate temporal profile during drug delivery. (a) Representative example of the flowrate temporal profile obtained from the numerical, semianalytical slow, and semianalytical slow + fast solutions for a bioelectronic device when the function f(V) is obtained from the finite element analysis (FEA) using the Marlow hyperelastic model. The maximum flowrate is labeled as the peak value of the flowrate temporal profile. (b) Representative example of the flowrate temporal profile showing the analytical slow + fast solution where the function f(V) is obtained from bending-dominated deformation. The dimensions of the flexible membrane are thickness h = 150 μm and radius R₀ = 1.20 mm. The electrical current is 0.5 mA, and the cross section of the microchannels is 50 μm. The three nondimensional values are M^∗ = 0.0009, P₀^∗ = 0.1013, and V₀^∗ = 0.9162.

Figure 4

Maximum flowrate. (a) Drug delivery temporal flowrate showing the maximum (peak) flowrate value when the electrical current changes from 0.10 mA to 1.00 mA. (b) Maximum flowrate as a function of the electrical current. The dimensions of the flexible membrane are thickness h = 150 μm and radius R₀ = 1.20 mm. The cross section of the microchannels is 50 μm. The two nondimensional values are P₀^∗ = 0.1013 and V₀^∗ = 0.9162.

Figure 5

Parametric study of the maximum flowrate. Changes in the maximum flowrate when (a) the microchannel cross section is reduced from 50 μm to 18 μm which increases the nondimensional parameter M^∗, (b) the electrolyte chamber goes from full to partially full (50%) which introduces an initial gas volume via the nondimensional parameter V₀^∗, and (c) the initial environmental pressure in the tissue/organ changes which affects the nondimensional parameter P₀^∗. The dimensions of the flexible membrane are thickness h = 150 μm  and radius R₀ = 1.20 mm.