Interacting-heads motif explains the X-ray diffraction pattern of relaxed vertebrate skeletal muscle

Abstract

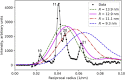
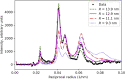
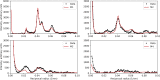
Electron microscopy (EM) shows that myosin heads in thick filaments isolated from striated muscles interact with each other and with the myosin tail under relaxing conditions. This "interacting-heads motif" (IHM) is highly conserved across the animal kingdom and is thought to be the basis of the super-relaxed state. However, a recent X-ray modeling study concludes, contrary to expectation, that the IHM is not present in relaxed intact muscle. We propose that this conclusion results from modeling with a thick filament 3D reconstruction in which the myosin heads have radially collapsed onto the thick filament backbone, not from absence of the IHM. Such radial collapse, by about 3-4 nm, is well established in EM studies of negatively stained myosin filaments, on which the reconstruction was based. We have tested this idea by carrying out similar X-ray modeling and determining the effect of the radial position of the heads on the goodness of fit to the X-ray pattern. We find that, when the IHM is modeled into a thick filament at a radius 3-4 nm greater than that modeled in the recent study, there is good agreement with the X-ray pattern. When the original (collapsed) radial position is used, the fit is poor, in agreement with that study. We show that modeling of the low-angle region of the X-ray pattern is relatively insensitive to the conformation of the myosin heads but very sensitive to their radial distance from the filament axis. We conclude that the IHM is sufficient to explain the X-ray diffraction pattern of intact muscle when placed at the appropriate radius.

Figure 1

X-ray diffraction pattern of relaxed, permeabilized plaice muscle. Half-mirrored pattern shows equator (Eq), meridian (Mer), and main myosin layer lines (M1–M6). Numerals 10, 11, 20, and 21 indicate sampling of M1 by equatorial reflections 10, 11, 20, and 21. Beam stop is shifted slightly off center to expose sampling of 10 reflection on right side of M1 layer line.

Figure 2

Myosin filament lattice in fish muscle (perspective view). Myosin filaments show P, C, and D zones (green, red, and blue, respectively) (39). One unit cell of hexagonal lattice (side a) is shaded in gray. φ is angle of rotation of filament within unit cell; all filaments in simple lattice have same rotation. Springs represent inter-filament connections formed by M-line proteins at center of sarcomere. The deviation of the center of a filament from its ideal position in the lattice is controlled by the stiffness of these connections, causing disorder of the second kind (40), characterized by the standard deviations of the neighboring filaments in a plane perpendicular to, or along, the filament axis (Δr, Δz, respectively); dotted ellipse indicates that Δr can be in any radial direction. To see this figure in color, go online.

Figure 3

Effect of the fraction of helically perturbed myosin heads on the M1 intensity from a myosin filament. Intensity is strongest with no perturbation (f = 0; all myosin heads organized in ideal helix). With varying numbers of heads lying on a perturbed helix (the arrangement found in the C zone) (6,9), intensities are weaker but similar, and remain in the same position radially. Thus, the perturbation has only a minor effect on the modeling. We used f = 0.67, for subsequent modeling. See also Fig. S2. To see this figure in color, go online.

Figure 4

Effect of radial position of myosin heads on M1 intensity. Calculation of diffraction from a single myosin filament (f = 0.67) shows that radial distance of COM of IHMs from filament axis dramatically affects the radial position (i.e., along x axis) of diffracted intensity. When the COM of the IHM (PDB: 3jbh) is at R = 13.9 nm (green), intensity occurs roughly over observed intensity in the X-ray pattern (black squares; cf. M1 of Fig. 1). At lower radii (11.3 nm and 9.3 nm) the observed intensity is not well accounted for. The best match appears to be in the range 13–14 nm. Calculated intensities were scaled by the same factor compared with the observed data. Numerals 10, 11, 20, and 21 indicate indices of sampled reflections in X-ray data. See also Fig. S3. To see this figure in color, go online.

Figure 5

Effects of radial (A) and axial (B) disorder on calculated M1 intensity. (A) Radial disorder (Δr) affects primarily the sharpness and separation of the sampled peaks on M1. (B) Axial disorder (Δz) has little effect on M1, but affects meridional intensity on M3 and M6 (Fig. S4). Other parameters: f = 0.67; R = 12.9 nm, φ = 37°. In (A) Δz = 2 nm; M1 R-factors were 0.521, 0.053, and 0.064 for Δr = 1 nm, 3 nm, and 4 nm respectively. In (B) Δr = 3 nm; M1 R-factors were 0.053, 0.040 and 0.039 for Δz = 2 nm, 3 nm, and 4 nm respectively. See also Fig. S4. To see this figure in color, go online.

Figure 6

Effect of radial position of myosin heads on M1 intensity in sampled diffraction pattern. Same models as in Fig. 4, but here placed in filament lattice, giving rise to diffraction peaks due to sampling of single-filament transforms by the lattice. Best match is for R ∼13.5 nm. For this simulation, f = 0.67, Δr = 3.5 nm, Δz = 2.5 nm, and φ = 37°. R-factors for M1 were 0.023, 0.042, 0.268, and 0.551 in order of descending R. See also Fig. S5. To see this figure in color, go online.

Figure 7

Effect of myosin filament rotation about long axis, φ, on M1 intensity. f = 0.67; R = 13.5 nm. Δr = 3.5 nm, Δz = 2.5 nm. R-factors were 0.164 (φ = 0°), 0.098 (φ = 15°), and 0.022 (φ = 30°). Thus, the best match to the data was obtained with a rotation of ∼30°. See also Fig. S6. To see this figure in color, go online.

Figure 8

R-factor calculated for best model, with Δr = 3.5 nm, Δz = 2.5 nm, and f = 0.67. (A) R is set to 13.5 nm and rotation angle φ is varied. Best R-factor obtained for φ = 37° (see Fig. 7). (B) φ set to 37°, and IHM COM varied. Best R-factor obtained for R ∼13.5 nm. Traces are shown for M1 alone (the strongest layer line, blue) and for the first four layer lines together (purple). Traces are also shown for the same model but where disorder in crown 2 and the ideal regions has been simulated by replacing the head pairs with 5-nm radius spheres (see text), improving the R-factor (Mix = mixed model; green and red traces; see also Fig. 9). To see this figure in color, go online.

Figure 9

Effect of partial disordering of crown 2 and ideal region head pairs on myosin layer line intensities M1–M4. Compare with Figs. S5 and S6. Disordering has little effect on the fitting of M1 but substantially improves the fit to the off-meridional portions of M2 and M3, reflected in the improved R-factor seen in Fig. 8. Data: squares, black lines; calculation with f = 0.67; R = 13.4 nm. Δr = 3.5 nm, Δz = 2.5 nm, and φ = 37° (red lines). Disordered pairs of myosin heads in crown 2 and in the ideal zone were modeled by spheres of 5-nm radius with centers at the same radial and axial positions as the COM of the heads in the IHM. The R-factor for M1 = 0.018 and for M1–M4, 0.047 (Fig. 8B). To see this figure in color, go online.

Figure 10

Effect of replacing IHMs with spheres on calculated M1 intensity. A thick-filament model was constructed where spheres of 5-nm radius replaced the IHMs, to determine whether diffraction was sensitive to the shape of the diffracting unit. Here, R = 13.6 nm, Δr = 3.5 nm, Δz = 2.5 nm, f = 0.67, φ = 37°, and sphere radius (Rsph) = 5 nm. The R-factor for this model was 0.020 for M1. See also Fig. S7. To see this figure in color, go online.