Time crystal dynamics in a weakly modulated stochastic time delayed system

Abstract

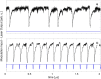
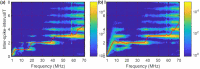
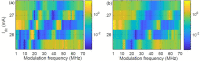
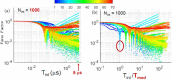
Time crystal oscillations in interacting, periodically driven many-particle systems are highly regular oscillations that persist for long periods of time, are robust to perturbations, and whose frequency differs from the frequency of the driving signal. Making use of underlying similarities of spatially-extended systems and time-delayed systems (TDSs), we present an experimental demonstration of time-crystal-like behavior in a stochastic, weakly modulated TDS. We consider a semiconductor laser near threshold with delayed feedback, whose output intensity shows abrupt spikes at irregular times. When the laser current is driven with a small-amplitude periodic signal we show that the interaction of delayed feedback and modulation can generate long-range regularity in the timing of the spikes, which lock to the modulation and, despite the presence of noise, remain in phase over thousands of modulation cycles. With pulsed modulation we find harmonic and subharmonic locking, while with sinusoidal modulation, we find only subharmonic locking, which is a characteristic feature of time-crystal behavior.

Figure 1

Laser intensity without modulation (a) and with pulsed modulation (b). In both panels the dc value of the laser current is $I_{\mathit{dc}}$=26 mA. In (b) the modulation amplitude is 0.631 mA ($\sim$2.4% of $I_{\mathit{dc}}$) and the frequency is $f_{\mathit{mod}}=7$ MHz. The pulsed modulation generates periodic spikes that are harmonically locked to the modulation; however, in between the spikes, the intensity fluctuations are irregular.

Figure 2

Inter-spike-interval (ISI) distribution in log color code for pulsed (a) and for sinusoidal (b) modulation, as a function of the modulation frequency; other parameters are as in Fig. 1b. The solid line indicates the mean ISI normalized to the modulation period. The plateau at low frequencies for pulsed modulation [panel (a)] where $〈\text{ISI}〉/T_{\mathit{mod}}=1$ is not seen in panel (b), where the modulation is sinusoidal.

Figure 3

Fano factor (in log color code) versus the modulation frequency and the dc value of the laser current, $I_{\mathit{dc}}$, for pulsed (a) and for sinusoidal (b) modulation. The blue region located at low frequencies in panel (a), where the spikes are 1:1 locked to the modulation is not seen in panel (b).

Figure 4

(a) Fano factor versus the duration of the counting interval, $T_{\text{int}}$. The modulation is pulsed, $I_{\mathit{dc}}=26$ mA, and the color code indicates the modulation frequency in MHz. (b) F versus $T_{\text{int}}$ normalized to the period of the modulation, $T_{\mathit{mod}}$ (i.e., F vs. the number of modulation periods contained in the counting interval). F decreases sharply when $T_{\text{int}}/T_{\mathit{mod}}=n$ with $n\ge 1$.

Figure 5

(a) Fano factor vs. the number of modulation periods contained in the counting interval, $T_{\text{int}}/T_{\mathit{mod}}$. The experimental parameters are as in Fig. 4b, but the modulation waveform is sinusoidal. (b) F is computed from the shuffled sequence of spikes. In both panels, F dips when $T_{\text{int}}/T_{\mathit{mod}}=n$ with $n\ge 2$.

Figure 6

Comparison of different long-term locked behaviors when $I_{\mathit{dc}}=26$ mA and the frequency of the sinusoidal modulation is 25 MHz (a, c, e), 23 MHz (b, d, f). (a), (b) Short segment of the intensity time series; (c), (d) F versus $T_{\text{int}}/T$; (e), (f) spatio-temporal representation of the intensity time series: all the intensity values $\{I_i,i=1\cdots {10}^7\}$, are plotted in color code versus t and n such that $i=n\mathrm{\Delta }T+t$ and $\mathrm{\Delta }T$=2 $\mathrm{\mu }$s.

Figure 7

Fano factor of the sequence of spikes generated by sinusoidal modulation with $f_{\mathit{mod}}=25$ MHz and $I_{\mathit{dc}}=26$ mA. In (a) F is calculated from the original spike sequence and in (b) from the shuffled one, using $N_{\text{int}}=$10, 100 or 1000 spike counting intervals. To represent $F=0$ in log scale, we set it to $F={10}^{-5}$.