First demonstration of tuning between the Kitaev and Ising limits in a honeycomb lattice

Abstract

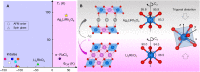
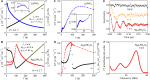
Recent observations of novel spin-orbit coupled states have generated interest in 4d/5d transition metal systems. A prime example is the [Formula: see text] state in iridate materials and α-RuCl₃ that drives Kitaev interactions. Here, by tuning the competition between spin-orbit interaction (λ_SOC) and trigonal crystal field (Δ_T), we restructure the spin-orbital wave functions into a previously unobserved [Formula: see text] state that drives Ising interactions. This is done via a topochemical reaction that converts Li₂RhO₃ to Ag₃LiRh₂O₆. Using perturbation theory, we present an explicit expression for the [Formula: see text] state in the limit Δ_T ≫ λ_SOC realized in Ag₃LiRh₂O₆, different from the conventional [Formula: see text] state in the limit λ_SOC ≫ Δ_T realized in Li₂RhO₃. The change of ground state is followed by a marked change of magnetism from a 6 K spin-glass in Li₂RhO₃ to a 94 K antiferromagnet in Ag₃LiRh₂O₆.

Fig. 1.. Phase diagram.

(A) Critical temperature (T_c) plotted against the Curie-Weiss temperature (${\mathrm{\Theta }}_{\text{CW}}^{\text{avg}}$) using the data in table S1 for polycrystalline 2D Kitaev materials. Circles and triangles represent AFM and spin-glass transitions, respectively. The iridate materials are (from left to right) Cu₃LiIr₂O₆, Ag₃LiIr₂O₆, Na₂IrO³, Cu₃NaIr₂O₆, Cu₂IrO₃, H₃LiIr₂O₆, and α-Li₂IrO₃. (B) Structural relationship between the first- and second-generation Kitaev systems, Li₂RhO₃ and Ag₃LiRh₂O₆, with enhanced trigonal distortion in the latter, as evidenced by the change of bond angles after cation exchange.

Fig. 2.. Magnetic characterization.

Magnetic susceptibility plotted as a function of temperature and Curie-Weiss analysis presented in (A) Li₂RhO₃ (blue) and (B) Ag₃LiRh₂O₆ (red). The ZFC and FC data are shown as full and empty symbols, respectively. Heat capacity as a function of temperature in (C) Li₂RhO₃ and (D) Ag₃LiRh₂O₆. The black circles in (D) show the derivative of magnetic susceptibility with respect to temperature. (E) μSR asymmetry plotted as a function of time in Ag₃LiRh₂O₆. For clarity, the curves at 100 and 80 K are offset with respect to the 1.5 K spectrum. The solid line is a fit to a Bessel function (see the Supplementary Materials for details). (F) Fourier transform of the μSR spectrum at 1.5 K showing two frequency components.

Fig. 3.. Wave functions.

(A) The J_eff = 1/2 limit, realized in Li₂RhO₃, where λ_SOC ≫ Δ_T. The probability density is visualized for the isospin-up wave function. (B) The Ising limit, realized in Ag₃LiRh₂O₆, where Δ_T ≫ λ_SOC. The probability density is visualized for the spin-up wave function. Notice the cubic and trigonal symmetries of the J_z and μ_z orbitals, respectively.

Fig. 4.. X-ray absorption spectroscopy.

(A) XAS data from Rh L_2,3 edges of Li₂RhO₃. The data were modeled with a step and two Gaussian functions for the L₃ edge (inset) and one Gaussian function for the L₂ edge. (B) Similar data and fits for the Rh L_2,3 edges of Ag₃LiRh₂O₆. (C) Theoretically calculated traces of projector products are tabulated and plotted for both the ideal limits (empty symbols) and real materials (full symbols).