Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 Mar 17;8(3):76.
doi: 10.3390/jimaging8030076.

Microsaccades, Drifts, Hopf Bundle and Neurogeometry

Dmitri Alekseevsky  1   2
Affiliations

Microsaccades, Drifts, Hopf Bundle and Neurogeometry

Dmitri Alekseevsky. J Imaging. .

Abstract

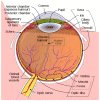
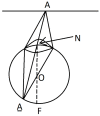
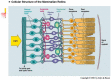
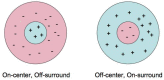
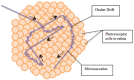
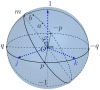
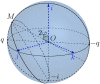
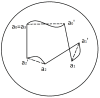
The first part of the paper contains a short review of the image processing in early vision is static, when the eyes and the stimulus are stable, and in dynamics, when the eyes participate in fixation eye movements. In the second part, we give an interpretation of Donders' and Listing's law in terms of the Hopf fibration of the 3-sphere over the 2-sphere. In particular, it is shown that the configuration space of the eye ball (when the head is fixed) is the 2-dimensional hemisphere SL+, called Listing hemisphere, and saccades are described as geodesic segments of SL+ with respect to the standard round metric. We study fixation eye movements (drift and microsaccades) in terms of this model and discuss the role of fixation eye movements in vision. A model of fixation eye movements is proposed that gives an explanation of presaccadic shift of receptive fields.

Keywords: Donders’ and Listing’s law; Hopf bundle; drift; fixation eyes movements; microsaccades; neurogeometry; quaternions; remapping; shift of receptive fields.

PubMed Disclaimer

Conflict of interest statement

The author declares no conflict of interest.

Figures

Figure 1
Figure 1
The Human Eye. Adapted from Wikipedia.
Figure 2
Figure 2
Central projection.
Figure 3
Figure 3
Anatomy of retina.
Figure 4
Figure 4
On and Off Kuffler cells.
Figure 5
Figure 5
Action of Marr filter.
Figure 6
Figure 6
Eye, retina and fovea. Adapted from Wikipedia.
Figure 7
Figure 7
(A) An example of an eye trace taken from an AOSLO movie. A microsaccade (magenta background) is clearly distinguishable from the ocular drift (blue background). Gray vertical gridlines demarcate frame boundaries from the AOSLO movie. Each frame is acquired over 33 ms as indicated by the scale bar. (B) An example of an image/frame from an AOSLO movie. The cone mosaic can be resolved even at the fovea. (C) An example of the AOSLO raster with a green letter E as it would appear to the subject. The small discontinuities in the eye trace at the boundaries between frames 478–479 and 480–481 are likely the result of tracking errors that occur at the edges of the frame. They are infrequent and an example is included here for full disclosure. Errors like this contribute to the peaks in the amplitude spectrum at the frame rate and higher harmonics. All original eye motion traces are available for download. Adapted from [43].
Figure 8
Figure 8
Microsaccades and Ocular Drifts. Adapted from Wikipedia https://commons.wikimedia.org/wiki, CC-BY.
Figure 9
Figure 9
Listing’s sphere.
Figure 10
Figure 10
The eye sphere.
Figure 11
Figure 11
Hexagone.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Bressloff P.C., Cowan J.D. A spherical model for orientation as spatial-frequency tuning in a cortical hypercolumn. Philos. Trans. R. Soc. Lond. B. 2003;357:1643–1667. doi: 10.1098/rstb.2002.1109. - DOI - PMC - PubMed
    1. Bressloff P.C., Cowan J.D. The functional geometry of local and horizontal connections in a model of V1. J. Physiol. Paris. 2003;97:221–236. doi: 10.1016/j.jphysparis.2003.09.017. - DOI - PubMed
    1. Bressloff P.C., Cowan J.D. The visual cortex as a crystal. Phys. D. 2002;173:226–258. doi: 10.1016/S0167-2789(02)00677-2. - DOI
    1. Citti G., Sarti A., editors. Neuromathematics of Vision. Springer; Berlin/Heidelberg, Germany: 2014. Lecture Notes in Morphogenesis.
    1. Petitot J. The neurogeometry of pinwheels as a sub-Riemannian contact structure. J. Physiol. Paris. 2003;97:265–309. doi: 10.1016/j.jphysparis.2003.10.010. - DOI - PubMed

LinkOut - more resources