Isotope-assisted metabolic flux analysis as an equality-constrained nonlinear program for improved scalability and robustness

Abstract

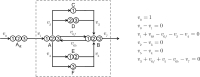
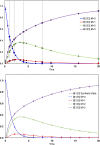
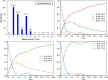
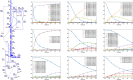
Stable isotope-assisted metabolic flux analysis (MFA) is a powerful method to estimate carbon flow and partitioning in metabolic networks. At its core, MFA is a parameter estimation problem wherein the fluxes and metabolite pool sizes are model parameters that are estimated, via optimization, to account for measurements of steady-state or isotopically-nonstationary isotope labeling patterns. As MFA problems advance in scale, they require efficient computational methods for fast and robust convergence. The structure of the MFA problem enables it to be cast as an equality-constrained nonlinear program (NLP), where the equality constraints are constructed from the MFA model equations, and the objective function is defined as the sum of squared residuals (SSR) between the model predictions and a set of labeling measurements. This NLP can be solved by using an algebraic modeling language (AML) that offers state-of-the-art optimization solvers for robust parameter estimation and superior scalability to large networks. When implemented in this manner, the optimization is performed with no distinction between state variables and model parameters. During each iteration of such an optimization, the system state is updated instead of being calculated explicitly from scratch, and this occurs concurrently with improvement in the model parameter estimates. This optimization approach starkly contrasts with traditional "shooting" methods where the state variables and model parameters are kept distinct and the system state is computed afresh during each iteration of a stepwise optimization. Our NLP formulation uses the MFA modeling framework of Wiechert et al. [1], which is amenable to incorporation of the model equations into an NLP. The NLP constraints consist of balances on either elementary metabolite units (EMUs) or cumomers. In this formulation, both the steady-state and isotopically-nonstationary MFA (inst-MFA) problems may be solved as an NLP. For the inst-MFA case, the ordinary differential equation (ODE) system describing the labeling dynamics is transcribed into a system of algebraic constraints for the NLP using collocation. This large-scale NLP may be solved efficiently using an NLP solver implemented on an AML. In our implementation, we used the reduced gradient solver CONOPT, implemented in the General Algebraic Modeling System (GAMS). The NLP framework is particularly advantageous for inst-MFA, scaling well to large networks with many free parameters, and having more robust convergence properties compared to the shooting methods that compute the system state and sensitivities at each iteration. Additionally, this NLP approach supports the use of tandem-MS data for both steady-state and inst-MFA when the cumomer framework is used. We assembled a software, eiFlux, written in Python and GAMS that uses the NLP approach and supports both steady-state and inst-MFA. We demonstrate the effectiveness of the NLP formulation on several examples, including a genome-scale inst-MFA model, to highlight the scalability and robustness of this approach. In addition to typical inst-MFA applications, we expect that this framework and our associated software, eiFlux, will be particularly useful for applying inst-MFA to complex MFA models, such as those developed for eukaryotes (e.g. algae) and co-cultures with multiple cell types.

Fig 1. Several factors make eiFlux unique among currently available MFA software.

eiFlux uses equality-constrained nonlinear programming to solve both the steady-state and inst-MFA problems. Treating the ODE system using collocation in an NLP formulation results in robust convergence properties. eiFlux, which supports the cumomer modeling approach, may directly fit tandem MS data.

Fig 2. The first six iterations of a generic reduced gradient algorithm are shown for a simple illustrative example (see S1 Text for details).

At each iteration of a reduced gradient algorithm, the variables are propagated to an improved point in which the constraints remain feasible. In this example, the feasible region (shaded in blue) lies above constraint g₁ and below constraint g₂. In this case, the iterations proceed along the g₁ nonlinear constraint boundary.

Fig 3. Toy network showing reactions and carbon atom rearrangements with stoichiometric flux constraints.

The dashed gray line indicates the cell boundary. Since v₀ is assumed to be known exactly, there are three independent fluxes based on the stoichiometric constraints. There are also six intracellular pool size parameters.

Fig 4

(Top) Continuous approximation to the DLS generated by fitting the synthetic measurements. The markers indicate the collocation points of the 5^th-order Radau IIA method, with the larger markers indicating the endpoint of each time interval (which are also collocation points in Radau IIA methods). The vertical dashed lines indicate the boundaries of each time interval. (Bottom) The fit to the synthetic data is shown, with a standard deviation of 0.01 arbitrarily assigned to each synthetic measurement. The synthetic data was generated by numerically solving the cumomer balances with a known flux and pool size distribution using the 4^th-order explicit Runge-Kutta method and a time step of 0.02. The continuous approximation generated by the 5^th-order Radau IIA collocation method fitting the synthetic measurements is superimposed for comparison. Clearly, using the collocation method the synthetic measurements are accurately fit by the model, and the continuous approximation accurately matches the synthetic data.

Fig 5. The result of assigning a larger than permissible step size in the stiff region for the toy network.

The total measurement residuals converged upon by eiFlux when the time domain is divided into two intervals: [0, 10] and [10, 20] is plotted showing that the poor approximation in the first time interval does not significantly affect the solution in the later time interval. The solution is plotted for all measured fragments of B. Clearly, the solution is poorly approximated in the first time interval, but the solution in the second interval remains accurately approximated and asymptotically approaches the true steady-state solution.

Fig 6

(Left) The central carbon metabolic reactions of the E. coli model, generated using Escher. Not shown are peripheral reactions that produce biomass metabolites (amino acids). For a full list of network reactions and their associated carbon atom rearrangements, see S4 Text. (Right) A set of representative model fits to the simulated tandem MS measurement data of several metabolites. For the full set of model fits to all simulated data, see S4 Text.

Fig 7

(Left) Number of restarts out of 20 that converged within a vicinity (percent) of the best-computed optimum for the NLP approach and the shooting method. For the NLP approach, these 20 restarts were performed with the 3rd-order Radau IIA method followed by refinement using the 9th-order method. The best achieved optimum was 660.39 with the 3rd-order method and 644.14 after the 9th-order refinement. For the shooting method we used the software INCA, and the best achieved optimum was 646.34. (Right) Results from 100 restarts for the genome-scale Synechocystis example. Using the NLP approach, most optimizations started from a random initial point converge to within 10% of the best-computed optimal solution, and a large fraction within 2%. This highlights the robustness of the NLP approach for inst-MFA applications.