Spatial Manipulation of Particles and Cells at Micro- and Nanoscale via Magnetic Forces

Abstract

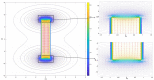
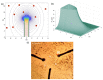
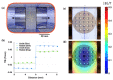
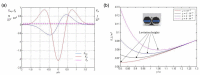
The importance of magnetic micro- and nanoparticles for applications in biomedical technology is widely recognised. Many of these applications, including tissue engineering, cell sorting, biosensors, drug delivery, and lab-on-chip devices, require remote manipulation of magnetic objects. High-gradient magnetic fields generated by micromagnets in the range of 10³-10⁵ T/m are sufficient for magnetic forces to overcome other forces caused by viscosity, gravity, and thermal fluctuations. In this paper, various magnetic systems capable of generating magnetic fields with required spatial gradients are analysed. Starting from simple systems of individual magnets and methods of field computation, more advanced magnetic microarrays obtained by lithography patterning of permanent magnets are introduced. More flexible field configurations can be formed with the use of soft magnetic materials magnetised by an external field, which allows control over both temporal and spatial field distributions. As an example, soft magnetic microwires are considered. A very attractive method of field generation is utilising tuneable domain configurations. In this review, we discuss the force requirements and constraints for different areas of application, emphasising the current challenges and how to overcome them.

Keywords: cell arraying; diamagnetic levitation; gradient magnetic field; magnetic force; micromagnetic array.

Figure 1

Principle directions and quantities for field calculations of a uniformly magnetised cylinder: (a) axial magnetisation; (b) diametrical magnetisation.

Figure 2

Magnetic induction configuration around a ferromagnetic cylinder with axial magnetisation. The calculations were performed for the following parameters: magnetisation $M=5·{10}^5$ A/m (Co-based alloys), cylinder radius $a=15 \mathsf{\mu }\mathrm{m},$ and length $2L=16 a$. Colour scale shows the magnitude of $\left|B\right| \mathrm{in} T$.

Figure 3

Magnetic induction configuration around ferromagnetic cylinder magnetised along the diameter. The parameters are the same as in Figure 2. Colour scale shows the magnitude of $\left|B\right| \mathrm{in} T$.

Figure 4

Hysteresis loops of amorphous microwires of Fe-based (Fe_77.5Si_7.5B₁₅) and Co-based (Co_67.5Fe_4.5B₁₄Si₁₁Cr₃) compositions magnetised by an axial field (a) and a perpendicular field (b). The axial and perpendicular curves were measured using an inductive method and vibrating sample magnetometry, respectively. Wires with a diameter of 20–25 microns have a glass coating with a thickness of 4–4.5 microns. The saturation magnetisation is 1.5 MA/m and 0.55 MA/m for Fe-based and Co-based wires, respectively. The wires have different anisotropies: axial for Fe-based and circumferential for Co-based, but both are magnetised along the axis by a small field below 150 A/m. A relatively small field of ~100 mT is required to induce a large perpendicular magnetisation of 0.5 MA/m in Fe-based wire.

Figure 5

(a) Schematic illustration of the paramagnetic particle capture and acceleration towards the wire. (b) Particle velocity as it moves towards the wire. For calculations, the field distribution in Figure 2 was used. As particles, cells (human hepatocellular carcinoma line (Huh7)) with internalised iron oxide NPs were considered [28]: $R_h=5 \mathsf{\mu }\mathrm{m},$ and the mass of magnetic NPs in the cell is 1 pg with the total volume of $0.2 {\mathsf{\mu }\mathrm{m}}^3$. Taking $\chi ={10}^4$ for a magnetic nanoparticle, the effective susceptibility of a cell is 2. $\eta =8.9 ·{10}^{-4}$ Pa $\times$ s (viscosity of water). (c) Distribution of iron oxide NPs around amorphous microwires of Co-based alloy with a diameter of 30 microns after the application of a small magnetic field that magnetises the wires along the axis. Areas around microwire edges are free from particles. Arrow R designates the size of particle-free area. Scale bar equals 200 µm. (c) is reprinted with permission from ref. [28]. Copyright 2020, Elsevier B.V.

Figure 6

Schematics of magnetic field configuration with two axially magnetised cylinders: (a,c) cylinders with the same magnetisation; (b,d) oppositely magnetised cylinders. Closely spaced magnets with the same polarisation produce a nearly uniform magnetic field between N and S poles, whilst the magnets with opposite polarisation have a zero-field point (between alike poles) in the centre of the magnet system. (e) Gradient of magnetic induction. Calculations in (c–e) were performed for typical permanent magnets (NdFeB magnets with the surface field of 0.66 T).

Figure 7

Magnetic field (a) and field gradient (b) distributions for two NdFeB magnets with opposite polarisation (magnet dimensions: 25 mm in diameter and height, 20 mm between the magnets). The surface field is 0.66 T. The magnetic device contains a sharp zero point surrounded by constant field gradients. (c,d) Images of the ferrofluid redistribution in acrylic wells placed between the magnet poles. Reprinted with permission from ref. [34]. Copyright 2020, American Chemical Society.

Figure 8

(a) Magnetic field configuration from a pair of cylindrical magnets polarised along the diameter. (b) Two-dimensional energy plot represented by the square of the magnetic field induction ($B^2$) from a pair of microwires in the x-z plane. $y/a=1$. The magnet parameters correspond to Co-based amorphous microwire (see Figure 4) with radius $a=10 \mathsf{\mu }\mathrm{m},$ length $2L=32a$, magnetisation $M=0.5 MA/m$, and distance between wires$d=3a$. (c) Distribution of $B^2$ along the wire length (z-axis) for two different lengths, $L/a=8 \mathrm{and} 16.$ $x=0 \mathrm{and} 0.5/a, y/a=1$. A saddle-shaped minimum with a wide plateau is formed between the wire edges, and the energy peaks near the edges are sharper with increasing length. Moving away from the center point on the x-axis reduces these peaks.

Figure 9

(a) Dependence of the y-component of magnetic force $F_{my}$ and the second derivative of the total energy $K_y={\partial }^{2}U/\partial y^2$ on height $y \mathrm{above} \mathrm{the} \mathrm{pair} \mathrm{in} \mathrm{the} \mathrm{symmetry} \mathrm{point}\left(x=0, z=0\right)$. Gravitational force density $F_g=g∆\rho =0.2\times {10}^4 \mathrm{N}/{\mathrm{m}}^3$ (with respect to suspension), $({\chi }_p-{\chi }_{ex})=-{10}^{-4}$. (b) Total energy density vs. the distance (y) for different values of the diamagnetic susceptibility. The position of levitation is indicated by arrows. The wire parameters correspond to Figure 8. Inset shows the levitation configuration.

Figure 10

Schematics of microfabrication process to produce grids of micromagnetic poles with NdFeB. (a) Silicon wafer is micropatterned using lithography and etching and coated with SiO₂ layer 100 nm thick, and then 100 nm thick Ta layer is sputtered to serve as a reaction barrier between SiO₂ and NdFeB; (b) 30 μm thick NdFeB layer is sputtered and coated with 500 nm Ta layer.

Figure 11

Schematics of micromagnetic arrays. (a) Basic system of uniformly magnetised cylinders (along the height or along the diameter); (b) uniformly magnetised magnetic film with voids that magnetically is equivalent to the combination of a uniform film and a system of cylinders magnetised oppositely to the film; (c) an array produced by thermomagnetic patterning corresponds to an array of closely spaced cylinders with mutually opposite magnetisation.

Figure 12

(a) Schematic configuration of a unit cell of arrays of cylindrical micromagnets. (b,c) Two-dimensional plots of the energy profile (per unit cell) represented by the square of the magnetic field induction ($B^2$) from arrays of cylindrical micromagnets with axial and diametric magnetisations, respectively, in the x-z plane. y/a = 0.7. The magnet parameters correspond to Co-based amorphous alloys with magnetisation ${\mu }_{0}M=0.6 T$, radius a = 15 μm, length 2L = 2a, and distance between magnets d_x = d_z = 2.5a.

Figure 13

Equipotential energy density $U$ (x = 0, y, z) for a periodic array of cylindrical magnets with in-plane magnetisation (Figure 12a,c). The total energy $U$ includes magnetic and gravity energies (Equation (33)). $g∆\rho =0.2\times {10}^4 \mathrm{N}/{\mathrm{m}}^3$; $({\chi }_p-{\chi }_{ex})=-0.5\times {10}^{-4}$. The change in the z-coordinate is shown along three micromagnets (depicted in the figure), and the graphical image can be periodically continued along the z-axis.

Figure 14

(a) Magnetic energy profile from an array of microwires magnetised along diameter (blue curves; red curves show the energy profile from a single wire) and schematics of paramagnetic NP distribution with a higher concentration near the wires. (b) Stationary distribution of concentration $\mathrm{c}/{\mathrm{c}}_0$ (normalised to initial concentration ${ \mathrm{c}}_0$) around a single microwire for different values of magnetic susceptibility. Inset shows the concentration distribution after a few characteristic times. $r/a$ is the normalised polar coordinate. The calculations were performed for the parameters:$D=3\times {10}^{-12}{\mathrm{m}}^2/\mathrm{s}$, $\mathsf{\chi }={10}^{-4} \left(for insert\right),$ $V={10}^{-21}{ \mathrm{m}}^3$, $a=15 \mathsf{\mu }\mathrm{m}$, and $M=0.5 \mathrm{MA}/\mathrm{m}.$

Figure 15

(a) Image of a uniaxial ferrite garnet film with magnetic domains having a spatial periodicity λ = 6.8 µm, visualised due to the polar Faraday effect. (b) Domain configuration under applied field. The lines above demonstrate the change in the potential landscape with the distance above the film. (c,d) Microscope snapshots of the trajectories of one particle with a diameter of 360 nm without the field and in the presence of the field, respectively. The dashed lines designate the position of the domain walls. Insets show the potential landscapes along y-direction. The scale bar is 5 µm. Reprinted with permission from ref. [71]. Copyright 2016, American Chemical Society.

Figure 16

(a) Effective coefficient of diffusion $D_{eff}$ measured across the domain walls of the ferrite garnet film (presented in Figure 15) as a function of the external field frequency for superparamagnetic particles with a diameter of 270 nm and susceptibility of 2. The field amplitude is 1200 A/m. The green dashed line represents the diffusion coefficient measured at a zero field. The frequency of the diffusion maximum $f_m$ = 14.5 Hz is close to the critical frequency $f_c$ = 13.4 Hz. The inset shows ${\sigma }_x^2\left(t\right)/2t$ for different frequencies marked in the main plot. The red line for $f_m$ is used to determine $D_{eff}$. (b) Schematic representation of the magnetic potential landscape for different frequencies. Reprinted with permission from ref. [72]. Copyright 2016, American Chemical Society.

Figure 17

Realising a travelling magnetic potential in a microwire with a circular domain structure by passing an alternating current through the wire.

Figure 18

Assessment of cell viability in the presence of microwires (a,c) in comparison with control samples without the wires (b,d). A nutrient medium with the cell culture—human embryonic fibroblasts (FEH-T)—was used. (a,b) After exposure for 24 h, fluorescent staining by ethidium bromide was used to assess the survival of cells in the presence and in the absence of microwires. Luminosity was examined under a fluorescent microscope. (c,d) Optical microscope images after 168-h exposure demonstrate no visual effect of microwires on cell viability.