Hierarchical Amplitude-Aware Permutation Entropy-Based Fault Feature Extraction Method for Rolling Bearings

Abstract

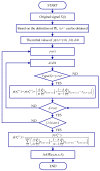
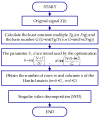
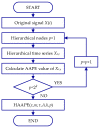
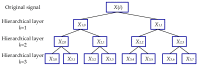
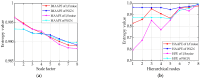
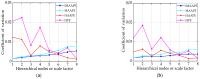
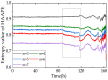
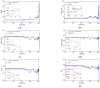
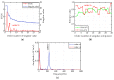
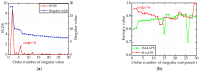
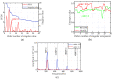
In order to detect the incipient fault of rolling bearings and to effectively identify fault characteristics, based on amplitude-aware permutation entropy (AAPE), an enhanced method named hierarchical amplitude-aware permutation entropy (HAAPE) is proposed in this paper to solve complex time series in a new dynamic change analysis. Firstly, hierarchical analysis and AAPE are combined to excavate multilevel fault information, both low-frequency and high-frequency components of the abnormal bearing vibration signal. Secondly, from the experimental analysis, it is found that HAAPE is sensitive to the early failure of rolling bearings, which makes it suitable to evaluate the performance degradation of a bearing in its run-to-failure life cycle. Finally, a fault feature selection strategy based on HAAPE is put forward to select the bearing fault characteristics after the application of the least common multiple in singular value decomposition (LCM-SVD) method to the fault vibration signal. Moreover, several other entropy-based methods are also introduced for a comparative analysis of the experimental data, and the results demonstrate that HAAPE can extract fault features more effectively and with a higher accuracy.

Keywords: fault feature extraction; hierarchical amplitude-aware permutation entropy; performance trend state assessment; rolling bearing.

Figure 1

Flowchart of the AAPE.

Figure 2

Flowchart of LCM-SVD.

Figure 3

Flowchart of the HAAPE method.

Figure 4

Hierarchical decomposition of original signal with three layers.

Figure 5

(a) Temporal waveform of WGN, and (b) temporal waveform of 1/f noise.

Figure 6

(a) Average of 50 sets of values of IMAAPE and MAAPE, and (b) average of 50 sets of values of HAAPE and HPE.

Figure 7

(a) CV values of four entropies for 1/f noise, and (b) CV values of four entropies for WGN.

Figure 8

(a) The experimental bench’s schematic diagram and (b) its physical diagram.

Figure 9

The influences of embedding dimensions on HAAPE.

Figure 10

Six indicators with performance degradation trend analysis over whole lifetime. (a) RMS; (b) Kurtosis; (c) HAAPE; (d) IMAAPE; (e)HPE and (f) PE.

Figure 11

(a) Time-domain waveform, and (b) Hilbert envelope spectrum of the 533rd data group with Gaussian noise.

Figure 12

Analysis diagram of 533rd data group with Gaussian noise. (a) DSUMSV, (b) HAAPE and IMAAPE, and (c) Hilbert envelope spectrum.

Figure 13

Analysis diagram of 534th data group with Gaussian noise. (a) DSUMSV, (b) HAAPE and IMAAPE, and (c) Hilbert envelope spectrum.

Figure 13

Analysis diagram of 534th data group with Gaussian noise. (a) DSUMSV, (b) HAAPE and IMAAPE, and (c) Hilbert envelope spectrum.

Figure 14

Analysis diagram of 700th data group with Gaussian noise. (a) DSUMSV, (b) HAAPE and IMAAPE, and (c) Hilbert envelope spectrum.