Tipping the Balance: A Criticality Perspective

Abstract

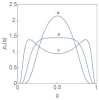
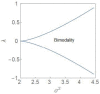
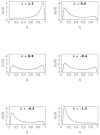
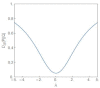
Cell populations are often characterised by phenotypic heterogeneity in the form of two distinct subpopulations. We consider a model of tumour cells consisting of two subpopulations: non-cancer promoting (NCP) and cancer-promoting (CP). Under steady state conditions, the model has similarities with a well-known model of population genetics which exhibits a purely noise-induced transition from unimodality to bimodality at a critical value of the noise intensity σ2. The noise is associated with the parameter λ representing the system-environment coupling. In the case of the tumour model, λ has a natural interpretation in terms of the tissue microenvironment which has considerable influence on the phenotypic composition of the tumour. Oncogenic transformations give rise to considerable fluctuations in the parameter. We compute the λ-σ2 phase diagram in a stochastic setting, drawing analogies between bifurcations and phase transitions. In the region of bimodality, a transition from a state of balance to a state of dominance, in terms of the competing subpopulations, occurs at λ = 0. Away from this point, the NCP (CP) subpopulation becomes dominant as λ changes towards positive (negative) values. The variance of the steady state probability density function as well as two entropic measures provide characteristic signatures at the transition point.

Keywords: bifurcations; bimodality; cancer; entropic measures; noise-induced transition; phase transitions; phenotypic heterogeneity; probability density function; stochastic potential; tumour population.

Figure 1

Steady state PDF, $p_S\left(q\right)$, versus $q$ for $\lambda =0.$ The noise intensity ${\sigma }^2$ has values 1.0 $\left(a\right)$, 2.0 $\left(b\right)$, and 4.0 $\left(c\right)$. A purely noise-induced transition from unimodality to bimodality occurs when the noise intensity exceeds the critical value ${\sigma }_c^2=2$.

Figure 2

Parametric plots of bifurcation curves (22) and (23) in the $\left(\lambda -{\sigma }^2\right)$ plane. The curves separate a region of bimodality from the regions of unimodality.

Figure 3

Hysteresis plots for $q_m$ and $1-q_m$ versus λ with ${\sigma }^2=4$. The two plots correspond to the two phenotypically distinct subpopulations.

Figure 4

Cumulative distribution function (CDF) of $q$ versus λ for the cases $\left(d\right) F_S\left(0.5\right)$ and $\left(e\right) 1-F_S\left(0.5\right)$ with ${\sigma }^2=8.0.$.

Figure 5

Evolution of the steady state PDF $P_S\left(q\right)$ versus $q$ as the parameter decreases from positive to negative values with ${\sigma }^2=4.0.$ The same set of plots represent the evolution of $P_S\left(1-q\right)$ versus $q$ but with the sign of λ changed.

Figure 6

Stochastic potential $\phi \left(q\right)$ (12) versus $q$ with ${\sigma }^2=4.0$.

Figure 7

The variance of the steady state probability distribution, given in (9), versus λ for ${\sigma }^2=4$.

Figure 8

The plot of $D_{JS}\left(P\left|\right|Q\right)$ versus λ. For the P-distribution, ${\sigma }^2=4, \lambda \ne 0$. For the Q-distribution, ${\sigma }^2=2, \lambda =0$, i.e., the distribution is the critical distribution.

Figure 9

The plot of $D_{JS}\left(P\left|\right|Q\right)$ versus λ. For both the distributions $P$ and $Q$, ${\sigma }^2=4$ but the λ values are opposite in sign.

Figure 10

The plot of $CPE$ (28) versus λ with ${\sigma }^2=4.0$. The entropic measure has the highest value at λ = 0.