Conditional Process Analysis for Effective Lens Position According to Preoperative Axial Length

Abstract

Purpose: To predict the effective lens position (ELP) using conditional process analysis according to preoperative axial length.

Setting: Yeouido St. Mary hospital.

Design: A retrospective case series.

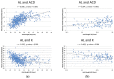
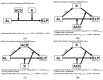
Methods: This study included 621 eyes from 621 patients who underwent conventional cataract surgery at Yeouido St. Mary Hospital. Preoperative axial length (AL), mean corneal power (K), and anterior chamber depth (ACD) were measured by partial coherence interferometry. AL was used as an independent variable for the prediction of ELP, and 621 eyes were classified into four groups according to AL. Using conditional process analysis, we developed 24 structural equation models, with ACD and K acting as mediator, moderator or not included as variables, and investigated the model that best predicted ELP.

Results: When AL was 23.0 mm or shorter, the predictability for ELP was highest when ACD and K acted as moderating variables (R2 = 0.217). When AL was between 23.0 mm and 24.5 mm or longer than 26.0 mm, the predictability was highest when K acted as a mediating variable and ACD acted as a moderating variable (R2 = 0.217 and R2 = 0.401). On the other hand, when AL ranged from 24.5 mm to 26.0 mm, the model with ACD as a mediating variable and K as a moderating variable was the most accurate (R2 = 0.220).

Conclusions: The optimal structural equation model for ELP prediction in each group varied according to AL. Conditional process analysis can be an alternative to conventional multiple linear regression analysis in ELP prediction.

Keywords: axial length; conditional process analysis; effective lens position; intraocular lens power calculation.

Figure 1

The relationships between axial length (AL) and other variables for structural equation models. (a) Total 621 eyes; (b) AL $\le$ 23.0 mm; (c) 23.0 mm < AL $\le$ 24.5 mm; (d) 24.5 mm < AL $\le$ 26.0 mm; (e) AL $>$ 26.0 mm. K = mean corneal dioptric power; ACD = anterior chamber depth.

Figure 1

The relationships between axial length (AL) and other variables for structural equation models. (a) Total 621 eyes; (b) AL $\le$ 23.0 mm; (c) 23.0 mm < AL $\le$ 24.5 mm; (d) 24.5 mm < AL $\le$ 26.0 mm; (e) AL $>$ 26.0 mm. K = mean corneal dioptric power; ACD = anterior chamber depth.

Figure 2

The structural equation models for the prediction of effective lens position (ELP) in each range of axial length (AL). (a) AL $\le$ 23.0 mm; (b) 23.0 mm < AL $\le$ 24.5 mm; (c) 24.5 mm < AL $\le$ 26.0 mm; (d) AL $>$ 26.0 mm. K = mean corneal dioptric power; ACD = anterior chamber depth.