Scaling the leaf length-times-width equation to predict total leaf area of shoots
- PMID: 35350072
- PMCID: PMC9445601
- DOI: 10.1093/aob/mcac043
Scaling the leaf length-times-width equation to predict total leaf area of shoots
Abstract
Background and aims: An individual plant consists of different-sized shoots, each of which consists of different-sized leaves. To predict plant-level physiological responses from the responses of individual leaves, modelling this within-shoot leaf size variation is necessary. Within-plant leaf trait variation has been well investigated in canopy photosynthesis models but less so in plant allometry. Therefore, integration of these two different approaches is needed.
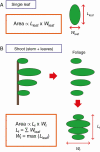
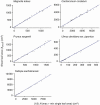
Methods: We focused on an established leaf-level relationship that the area of an individual leaf lamina is proportional to the product of its length and width. The geometric interpretation of this equation is that different-sized leaf laminas from a single species share the same basic form. Based on this shared basic form, we synthesized a new length-times-width equation predicting total shoot leaf area from the collective dimensions of leaves that comprise a shoot. Furthermore, we showed that several previously established empirical relationships, including the allometric relationships between total shoot leaf area, maximum individual leaf length within the shoot and total leaf number of the shoot, can be unified under the same geometric argument. We tested the model predictions using five species, all of which have simple leaves, selected from diverse taxa (Magnoliids, monocots and eudicots) and from different growth forms (trees, erect herbs and rosette herbs).
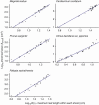
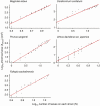
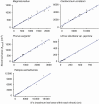
Key results: For all five species, the length-times-width equation explained within-species variation of total leaf area of a shoot with high accuracy (R2 > 0.994). These strong relationships existed despite leaf dimensions scaling very differently between species. We also found good support for all derived predictions from the model (R2 > 0.85).
Conclusions: Our model can be incorporated to improve previous models of allometry that do not consider within-shoot size variation of individual leaves, providing a cross-scale linkage between individual leaf-size variation and shoot-size variation.
Keywords: Cardiocrinum cordatum; Fallopia sachalinensis; Magnolia kobus; Prunus sargentii; Ulmus davidiana var. japonica; Allometry; Corner’s rule; intraspecific; leaf size; scaling; self-affine; shoot size.
© The Author(s) 2022. Published by Oxford University Press on behalf of the Annals of Botany Company.
Figures





Similar articles
-
How is light interception efficiency related to shoot structure in tall canopy species?Oecologia. 2017 Sep;185(1):29-41. doi: 10.1007/s00442-017-3926-0. Epub 2017 Aug 11. Oecologia. 2017. PMID: 28801737
-
Constraints on light interception efficiency due to shoot architecture in broad-leaved Nothofagus species.Tree Physiol. 2004 Jun;24(6):617-30. doi: 10.1093/treephys/24.6.617. Tree Physiol. 2004. PMID: 15059762
-
Geographic variation in shoot traits and branching intensity in relation to leaf size in Fagus crenata: A common garden experiment.Am J Bot. 2015 Jun;102(6):878-87. doi: 10.3732/ajb.1400559. Epub 2015 Jun 12. Am J Bot. 2015. PMID: 26101414
-
Photosynthesis and resource distribution through plant canopies.Plant Cell Environ. 2007 Sep;30(9):1052-71. doi: 10.1111/j.1365-3040.2007.01683.x. Plant Cell Environ. 2007. PMID: 17661747 Review.
-
Prophyll in Monocots: The Starting Point of Lateral Shoot Phyllotaxis.Front Plant Sci. 2022 Apr 13;13:855146. doi: 10.3389/fpls.2022.855146. eCollection 2022. Front Plant Sci. 2022. PMID: 35498710 Free PMC article.
Cited by
-
The Geometric Series Hypothesis of Leaf Area Distribution and Its Link to the Calculation of the Total Leaf Area per Shoot of Sasaella kongosanensis 'Aureostriatus'.Plants (Basel). 2024 Dec 29;14(1):73. doi: 10.3390/plants14010073. Plants (Basel). 2024. PMID: 39795333 Free PMC article.
-
Using the Montgomery-Koyama-Smith equation to calculate the stomatal area per unit lamina area for 12 Magnoliaceae species.Ann Bot. 2024 Dec 31;134(7):1151-1164. doi: 10.1093/aob/mcae165. Ann Bot. 2024. PMID: 39279221
-
Scaling relationships between the total number of leaves and the total leaf area per culm of two dwarf bamboo species.Ecol Evol. 2024 Jul 15;14(7):e70002. doi: 10.1002/ece3.70002. eCollection 2024 Jul. Ecol Evol. 2024. PMID: 39015880 Free PMC article.
-
Testing the Validity of the Montgomery-Koyama-Smith Equation for Calculating the Total Petal Area per Flower Using Two Rosaceae Species.Plants (Basel). 2024 Dec 15;13(24):3499. doi: 10.3390/plants13243499. Plants (Basel). 2024. PMID: 39771198 Free PMC article.
-
Patterns of Leaf and Fruit Morphological Variation in Marginal Populations of Acer tataricum L. subsp. tataricum.Plants (Basel). 2024 Jan 21;13(2):320. doi: 10.3390/plants13020320. Plants (Basel). 2024. PMID: 38276777 Free PMC article.
References
-
- Anten NPR. 2016. Optimization and game theory in canopy models. In: Hikosaka K, Niinemets Ü, Anten NPR, eds. Canopy photosynthesis: from basics to applications. Dordrecht: Springer Netherlands, 355–377.
-
- APG IV. 2016. An update of the Angiosperm Phylogeny Group classification for the orders and families of flowering plants: APG IV. Botanical Journal of the Linnean Society 181: 1–20.
-
- Auguie B. 2017. https://CRAN.R-project.org/package=gridExtra.
Publication types
MeSH terms
Associated data
LinkOut - more resources
Full Text Sources
Other Literature Sources

