Applications of Coarse-Grained Models in Metabolic Engineering

Abstract

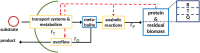
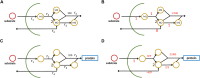
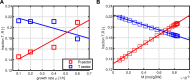
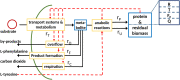
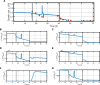
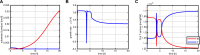
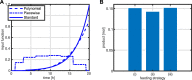
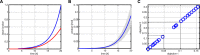
Mathematical modeling is a promising tool for better understanding of cellular processes. In recent years, the development of coarse-grained models has gained attraction since these simple models are able to capture and describe a broad range of growth conditions. Coarse-grained models often comprise only two cellular components, a low molecular component as representative for central metabolism and energy generation and a macromolecular component, representing the entire proteome. A framework is presented that presents a strict mass conservative model for bacterial growth during a biotechnological production process. After providing interesting properties for the steady-state solution, applications are presented 1) for a production process of an amino acid and 2) production of a metabolite from central metabolism.

Keywords: kinetic model; mathematical modeling; metabolic and gene regulatory networks; metabolic engineering; microbial growth; resource allocation; systems biotechnology.

FIGURE 1

General scheme of a coarse-grained model with partitioned proteome (ribosomal proteins R, proteins linked with the central metabolism T, and residual protein fraction Q) as the self-replicator system Scott et al. (2014); it consists of two components, indicated as blue boxes; (metabolite, low molecular weight), protein; and residual biomass (high molecular weight; protein is assumed to be 50% of total biomass). The pools are connected by a minimal set of reactions, indicated by yellow boxes, for substrate uptake, overflow metabolism, and protein synthesis.

FIGURE 2

Example network with metabolites M _i and reactions r _i ; conventional representation (A), new approach with one component representing protein/ biomass sector (C). On the right side (B,D), output data from the calculations are shown; it is to be noted that for the new approach, the dilution term must be taken into account which is not shown in the plot.

FIGURE 3

Relationship between the sectors T and R as a function of the specific growth rate μ. Experimental data are taken from the study by Schmidt et al., (2016) with protein representing 50% of the biomass (A). Estimated kinetics of first order for T/P and R/P as a function of variable M (B).

FIGURE 4

Specific growth rate μ as a function of substrate S, where the solid line represents the optimal case (A). Fractions R (red) and T (blue) as a function of the growth rate μ, where the solid line represents the optimal case, and dashed lines are from presented data in Figure 3B.

FIGURE 5

Scheme of the coarse-grained model expanded to include the formation of L-phenylalanine, respiration r _C , and residual biomass U.

FIGURE 6

Feeding profile of the process. Bioeactor volume V (A) and substrate concentration (glycerol) of the feed S _in (B) over the time course of the process, where vertical lines indicate the three process phases (batch phase, fed-batch phase, and production phase with constant feeding).

FIGURE 7

Comparison of the simulated quantities (solid blue line) against the experimental data (points) of the L-phenylalanine production process up to t = 71 h. Time course of the following concentrations: glycerol S (A), biomass X, L-tyrosine A (B), L-phenylalanine F (C), and acetate O as representative of the by-products of the process (D). The data points of L-tyrosine, which are negative due to insufficient measurement sensitivity, are set to zero.

FIGURE 8

Time course of intracellular concentrations of the L-phenylalanine process: metabolites M (A), mass fractions of proteins P (violet), and residual biomass U (orange) and metabolites M (blue), where M becomes negligible in the last process phase (B). Mass fractions of T (blue), R (red), and F (yellow) over the course of the process (C).

FIGURE 9

Time course of the simulated specific growth rate μ (blue) and the point-wise calculated specific growth rate obtained from experimental data indicated as orange dots (A), substrate transport rate r _T (B), protein synthesis rate r _P (C), overflow metabolism rate r _O (D), residual biomass synthesis rate r _U (E), product formation rate r _F (F), and respiration rate r _C (G).

FIGURE 10

Simulation outcome for the standard fed-batch process. Time course of substrate (blue) and product (red) in the medium (A). Growth rate μ (B). Time course of the protein sectors R (red) and T (blue) (C).

FIGURE 11

Comparison of the outcome of the three strategies. Time course for the feeding q _in as a function of time (A); value of the objective function (from left to right: standard feeding, polynomial function, and piece-wise function) (B).

FIGURE 12

Robust optimization. Input profile (red) for the robust case in comparison to the standard case (A). Product course of time for 100 simulations (in gray) with the variation in the maximal rate of the enzymatic processes and simulation with standard parameter (blue). (B). Pareto front for two objective functions: product amount at time t _end and total amount of the substrate needed to produce the product. Thin lines indicate the cost change for an increase in product amount as described in the text (C).