Polygenic risk for prostate cancer: Decreasing relative risk with age but little impact on absolute risk
- PMID: 35353984
- PMCID: PMC9118111
- DOI: 10.1016/j.ajhg.2022.03.008
Polygenic risk for prostate cancer: Decreasing relative risk with age but little impact on absolute risk
Abstract
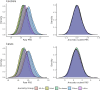
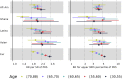
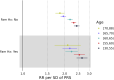
Polygenic risk scores (PRSs) for a variety of diseases have recently been shown to have relative risks that depend on age, and genetic relative risks decrease with increasing age. A refined understanding of the age dependency of PRSs for a disease is important for personalized risk predictions and risk stratification. To further evaluate how the PRS relative risk for prostate cancer depends on age, we refined analyses for a validated PRS for prostate cancer by using 64,274 prostate cancer cases and 46,432 controls of diverse ancestry (82.8% European, 9.8% African American, 3.8% Latino, 2.8% Asian, and 0.8% Ghanaian). Our strategy applied a novel weighted proportional hazards model to case-control data to fully utilize age to refine how the relative risk decreased with age. We found significantly greater relative risks for younger men (age 30-55 years) compared with older men (70-88 years) for both relative risk per standard deviation of the PRS and dichotomized according to the upper 90th percentile of the PRS distribution. For the largest European ancestral group that could provide reliable resolution, the log-relative risk decreased approximately linearly from age 50 to age 75. Despite strong evidence of age-dependent genetic relative risk, our results suggest that absolute risk predictions differed little from predictions that assumed a constant relative risk over ages, from short-term to long-term predictions, simplifying implementation of risk discussions into clinical practice.
Keywords: absolute risk prediction; genetic relative risk; weighted Cox regression.
Copyright © 2022 American Society of Human Genetics. Published by Elsevier Inc. All rights reserved.
Conflict of interest statement
Declaration of interests The authors declare no competing interests.
Figures



Similar articles
-
Validation of a multi-ancestry polygenic risk score and age-specific risks of prostate cancer: A meta-analysis within diverse populations.Elife. 2022 Jul 8;11:e78304. doi: 10.7554/eLife.78304. Elife. 2022. PMID: 35801699 Free PMC article.
-
Evaluating approaches for constructing polygenic risk scores for prostate cancer in men of African and European ancestry.Am J Hum Genet. 2023 Jul 6;110(7):1200-1206. doi: 10.1016/j.ajhg.2023.05.010. Epub 2023 Jun 12. Am J Hum Genet. 2023. PMID: 37311464 Free PMC article.
-
Polygenic risk scores for the prediction of common cancers in East Asians: A population-based prospective cohort study.Elife. 2023 Mar 27;12:e82608. doi: 10.7554/eLife.82608. Elife. 2023. PMID: 36971353 Free PMC article.
-
Implementation and implications for polygenic risk scores in healthcare.Hum Genomics. 2021 Jul 20;15(1):46. doi: 10.1186/s40246-021-00339-y. Hum Genomics. 2021. PMID: 34284826 Free PMC article. Review.
-
Polygenic risk scores for predicting outcomes and treatment response in psychiatry: hope or hype?Int Rev Psychiatry. 2022 Nov-Dec;34(7-8):663-675. doi: 10.1080/09540261.2022.2101352. Epub 2022 Jul 27. Int Rev Psychiatry. 2022. PMID: 36786114 Review.
Cited by
-
Aspartoacylase suppresses prostate cancer progression by blocking LYN activation.Mil Med Res. 2023 Jun 5;10(1):25. doi: 10.1186/s40779-023-00460-0. Mil Med Res. 2023. PMID: 37271807 Free PMC article.
-
Polygenic risk scores for prostate cancer: Comparative evaluations in UK and Australian cohorts.HGG Adv. 2025 Jul 7;6(4):100477. doi: 10.1016/j.xhgg.2025.100477. Online ahead of print. HGG Adv. 2025. PMID: 40629691 Free PMC article.
-
COL10A1 Facilitates Prostate Cancer Progression by Interacting With INHBA to Activate the PI3K/AKT Pathway.J Cell Mol Med. 2024 Dec;28(23):e70249. doi: 10.1111/jcmm.70249. J Cell Mol Med. 2024. PMID: 39656597 Free PMC article.
-
Combined CRISPRi and proteomics screening reveal a cohesin-CTCF-bound allele contributing to increased expression of RUVBL1 and prostate cancer progression.Am J Hum Genet. 2023 Aug 3;110(8):1289-1303. doi: 10.1016/j.ajhg.2023.07.003. Am J Hum Genet. 2023. PMID: 37541187 Free PMC article.
-
Implementing Reporting Standards for Polygenic Risk Scores for Atherosclerotic Cardiovascular Disease.Curr Atheroscler Rep. 2023 Jun;25(6):323-330. doi: 10.1007/s11883-023-01104-3. Epub 2023 May 24. Curr Atheroscler Rep. 2023. PMID: 37223852 Free PMC article. Review.
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

