Meta-programmable analog differentiator

Abstract

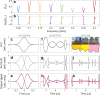
We present wave-based signal differentiation with unprecedented fidelity and flexibility by purposefully perturbing overmoded random scattering systems such that zeros of their scattering matrices lie exactly at the desired locations on the real frequency axis. Our technique overcomes limitations of hitherto existing approaches based on few-mode systems, both regarding their extreme vulnerability to fabrication inaccuracies or environmental perturbations and their inability to maintain high fidelity under in-situ adaptability. We demonstrate our technique experimentally by placing a programmable metasurface with hundreds of degrees of freedom inside a 3D disordered metallic box. Regarding the integrability of wave processors, such repurposing of existing enclosures is an enticing alternative to fabricating miniaturized devices. Our over-the-air differentiator can process in parallel multiple signals on distinct carriers and maintains high fidelity when reprogrammed to different carriers. We also perform programmable higher-order differentiation. Conceivable applications include segmentation or compression of communication or radar signals and machine vision.

Fig. 1. Operation principle of the meta-programmable analog temporal differentiator.

A signal $e\left(t\right)$ is modulated as envelope onto a carrier ${\omega }_0$ and incident via a guided single-mode channel on a disordered metallic electrically large box. The scattering properties of the latter can be tuned via programmable metasurfaces mounted on its walls such that the port’s reflection spectrum has a zero at the carrier frequency. Then, the port’s transfer function matches that of an ideal differentiator, displaying in the zero’s vicinity a linear V shape centered on ${\omega }_0$ as well as an abrupt $\pi$ phase jump at ${\omega }_0$ (see inset). Consequently, the reflected signal’s envelope is the temporal derivative of $e\left(t\right)$. Incident and reflected signals are separated via a circulator, see Supplementary Note 5 for details. A computer program digitally controls the realized differentiation operation by toggling between different metasurface configurations (color-coded) depending on the current needs in terms of the incident signal’s carrier frequency.

Fig. 2. Direct experimental results of meta-programmable analog temporal differentiation.

a, b Amplitude (a) and phase (b) of the system’s transfer function for eight different metasurface configurations (color-coded) that correspond to reflection zeros at eight equally spaced carrier frequencies in the 5-GHz band. c, f, i Envelopes $e\left(t\right)$ of experimentally injected waveforms corresponding to a Gaussian function (c), a set of quadratic polynomial functions (f), and a skyline of Rennes, France, composed of Basilique Saint-Sauveur, a traditional timber-framed house and Cathédrale Saint-Pierre (i). d, g, j Corresponding analytical derivatives $\frac{\mathrm{d}e\left(t\right)}{\mathrm{d}t}$. e, h, k Corresponding experimentally measured output signals. For a given waveform and carrier, the metasurface is toggled to the configuration optimized for this carrier, the input signal is injected, and the reflected signal is measured. The envelopes of the measured output signals for all eight considered carriers are superposed on these figures using the same colors to identify different carriers as in (a, b).

Fig. 3. Parallelization of meta-programmable wave-based differentiation.

a Principle of parallel computing with spectral degrees of freedom. The injected waveform is the sum of two signals (two independent envelopes $e_A\left(t\right)$ and $e_B\left(t\right)$ modulated onto distinct carriers ${\omega }_{1,A}$ and ${\omega }_{1,B}$) and the reflected signal is the sum of the derivatives of these two envelopes, modulated onto the respective carriers. b, c, f, g, j, k Amplitude and phase of the system’s transfer function for three examples (color-coded) of choices of two simultaneously imposed reflection zeros. The computer program can toggle between these by changing the metasurface configuration. d, e, h, i, l, m Envelope of experimentally measured output signal (spectrally bandpass-filtered around the respective carrier frequencies) upon injecting the indicated waveforms (see Supplementary Note 5 for details) in the three considered use cases.

Fig. 4. Meta-programmable second-order differentiator.

a Operation principle. Two setups akin to the one from Fig. 1 are cascaded (using circulators as shown) in order to implement the transfer function associated with an ideal second-order differentiator (see inset). Again, the computer program can toggle between metasurface configurations such that second-order derivatives of signal envelopes are computed for different carriers (color-coded). b–e, Examples of four experimentally measured use cases corresponding to the four distinct indicated carrier frequencies. In each case, amplitude and phase of the system’s transfer function are shown, as well as the experimentally measured output signal envelope upon injection of a Gaussian pulse. The displayed output signal envelopes are averaged over 20 acquisitions to alleviate the impact of measurement noise.