Geometry unites synchrony, chimeras, and waves in nonlinear oscillator networks

Abstract

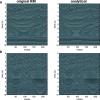
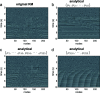
One of the simplest mathematical models in the study of nonlinear systems is the Kuramoto model, which describes synchronization in systems from swarms of insects to superconductors. We have recently found a connection between the original, real-valued nonlinear Kuramoto model and a corresponding complex-valued system that permits describing the system in terms of a linear operator and iterative update rule. We now use this description to investigate three major synchronization phenomena in Kuramoto networks (phase synchronization, chimera states, and traveling waves), not only in terms of steady state solutions but also in terms of transient dynamics and individual simulations. These results provide new mathematical insight into how sophisticated behaviors arise from connection patterns in nonlinear networked systems.

FIG. 1.

Analytical description of the transition to synchrony. Solutions of the original Kuramoto model (numerical simulation) (a) and the analytical evaluation (b) are plotted in color-code (dark tones indicate values close to $-\pi$ and light tones to $\pi$). As time evolves, the spatiotemporal dynamics become coherent and phase synchronization appears. A quantitative comparison between the two models is provided in Fig. S2. The level of synchronization, measured by the Kuramoto order parameter (c), starts at a low value with the random initial conditions and quickly approaches unity, which indicates the phase synchronized state of the system. The eigenmode contribution ( $\log |\mu |$) is plotted in color (d). The contribution of the first eigenmode, which represents zero phase difference across oscillators, dominates when the phase synchronized state appears.

FIG. 2.

Analytical description of the chimera state. Spatiotemporal dynamics for original KM (simulation) and analytical evaluation are plotted in color-code for the distance-dependent networks with $\varphi =1.15$ (a), and $\varphi =1.30$ (b). In these cases, chimera states are observed, where part of the network is synchronized and coexists with an incoherent region. Here, it is important to emphasize that the original KM and analytical expression are evaluated separately, using only the same initial condition. This demonstrates that the analytical approach is able to capture important details of the Kuramoto dynamics.

FIG. 3.

Geometry of eigenmodes explains the mechanism for the chimera state. The eigenmode contribution ( $\log |\mu |$) for increasing values of $\varphi$ at $t=1$ s (left) and $t=10$ s (middle) demonstrates the evolution of the first modes in the case of $\varphi =0$, while for $\varphi =1.30$, the first and last eigenmodes contribute in balance (right). Solid lines represent average eigenmode contribution over 100 simulations, and shaded regions represent standard deviation.

FIG. 4.

A subset of contributing eigenmodes creates an analytical approximation to the chimera state numerically simulated in the original KM (a). The first 10 eigenmodes $\{{\mu }_1,{\mu }_2,\dots ,{\mu }_{10}\}$ create a partially synchronized region that is too broad (b), while the last 10 eigenmodes $\{{\mu }_{216},{\mu }_{217},\dots ,{\mu }_{225}\}$ create no signature of a chimera (d). However, using the first 10 and last 10 eigenmodes $\{{\mu }_1,{\mu }_2,\dots ,{\mu }_{10},{\mu }_{216},{\mu }_{217},\dots ,{\mu }_{225}\}$ creates an analytical approximation to the chimera state (c).

FIG. 5.

Original KM (a) and analytical evaluation (b) for an example of a wave state on a ring graph ( $N=100,k=1$, see Sec. I E 2 in the supplementary material), resulting from a special set of initial conditions, a “twisted” state [see Eq. (27) in the supplementary material]. In this context, traveling wave states constitute the contribution of a single eigenmode to the dynamics ( $2^{\mathrm{nd}}$ eigenmode, in this case) (cf. Fig. S13). The Kuramoto order parameter (c) in the traveling wave state remains at $R=0$. However, when a finite perturbation is applied to the system at $t=2$ s, the network transitions to a phase synchronized state ( $R=1$). The relative instantaneous frequencies following the perturbation exhibit a non-trivial self-organized state during the transition to synchrony (c, inset). This transition is captured by the eigenmode contributions (d), where the $2^{\mathrm{nd}}$ eigenmode gives way to the $1^{\mathrm{st}}$ eigenmode when phase synchronization is reached.