A Coarse-Grained Model of Affinity Maturation Indicates the Importance of B-Cell Receptor Avidity in Epitope Subdominance

Abstract

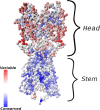
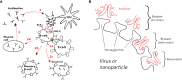
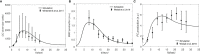
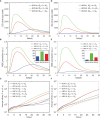
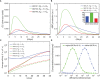
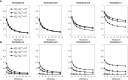
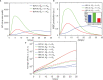
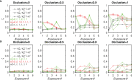
The elicitation of broadly neutralizing antibodies (bnAbs) is a major goal in the design of vaccines against rapidly-mutating viruses. In the case of influenza, many bnAbs that target conserved epitopes on the stem of the hemagglutinin protein (HA) have been discovered. However, these antibodies are rare, are not boosted well upon reinfection, and often have low neutralization potency, compared to strain-specific antibodies directed to the HA head. Different hypotheses have been proposed to explain this phenomenon. We use a coarse-grained computational model of the germinal center reaction to investigate how B-cell receptor binding valency affects the growth and affinity maturation of competing B-cells. We find that receptors that are unable to bind antigen bivalently, and also those that do not bind antigen cooperatively, have significantly slower rates of growth, memory B-cell production, and, under certain conditions, rates of affinity maturation. The corresponding B-cells are predicted to be outcompeted by B-cells that bind bivalently and cooperatively. We use the model to explore strategies for a universal influenza vaccine, e.g., how to boost the concentrations of the slower growing cross-reactive antibodies directed to the stem. The results suggest that, upon natural reinfections subsequent to vaccination, the protectiveness of such vaccines would erode, possibly requiring regular boosts. Collectively, our results strongly support the importance of bivalent antibody binding in immunodominance, and suggest guidelines for developing a universal influenza vaccine.

Keywords: germinal center; hemagglutinin; influenza; simulation; vaccination.

Figure 1

Influenza hemagglutinin (HA) spike protein colored by residue conservation. Sequences of avian, swine and human influenza type A spike proteins spanning the years 1918–2019 and subtypes 1-18 were downloaded from the NIH influenza research database (3); conservation was computed in MATLAB (4) after clustering the sequences to 97% identity and multiple alignment. The HA structure was taken from PDB entry 3LZG (5), and the image was generated using Visual Molecular Dynamics (6). Only the Cα atoms are shown.

Figure 2

Schematic of the GC model used in this study. (A) Model overview (1): B-cells are activated upon binding to antigen presented on follicular dendritic cells (FDCs, not explicitly modeled); (1a) in the optional T-cell help model (see text) B-cells are activated when the major histocompatibility complex receptor (MHCII) binds to the T-cell receptor (TCR); B-cell activation rescues B-cells from apoptosis, allowing them to mutate and proliferate (2); depending on the activation signal, B-cells can differentiate to plasma cells (2a), to memory B-cells (2b), or undergo apoptosis (2c) (3); Plasma cells secrete antibodies (Abs), which also compete with B-cell receptors for antigen (4), which is the essential aspect of the Ab feedback model (31) (see text). (B) Hypothetical modes of antibody binding to influenza spikes; bivalent binding without strain (top) corresponds to cooperative binding by antibody arms; bivalent binding with strain (middle) corresponds to noncooperative binding; monovalent binding (bottom) is assumed to be the dominant mode of binding of anti-HA stem antibodies (see Methods for details).

Figure 3

Comparison of simulation and experiments. (A) Total B-cells, (B) Memory B-cell production rate, (C) Plasma cell production rate. Experimental data for panel A was generated from the GC cross-sectional areas plotted in Figure S1B of (42), and converted to B cell counts as done in (43); The lower and upper error bars in panel (A) corresponds to 30% and 70% quantiles, respectively; experimental data for panels (B, C) was taken from Figure 4 of (43), who obtained raw data from Weisel et al. (44); the error bars in (B, C) correspond to approximately one SD.

Figure 4

Effect of antibody valency and epitope occlusion on GC properties. Left column (A–C) noninteracting B-cell case (o = 0); Right column (D–F) fully interacting B-cell case (o = 1); (A, D) Total B cells; (B, E) Memory cell production rate; insets: total MBC population at end of simulation; (C, F) Average affinity of B-cells and MBCs. For the definition of occlusion o, see Sec. 4.1.5.

Figure 5

Effect of initial affinity advantage on the growth of monovalent B-cells in the fully interacting B-cell case (o = 1). Panels (A–C) show the same quantities as Figures 4A–C ; The affinity distribution corresponding to BCR#1 was shifted toward higher values relative to BCR#2 and BCR#3 panel (D).

Figure 6

Fraction of MBC#1 (ζ, defined in the text) at the end of six GC simulations for different initial affinity advantage values vs. total number of BCR/Epitope pairs. (A) BCR#1 is cooperatively bivalent (K¹² _eq =10K¹¹ _eq); (B) BCR#1 is monovalent (K¹² _eq =0).

Figure 7

Effect of BCR valency and epitope concentration on GC evolution, with o = 1 (fully competitive case). Panels (A–C) show the same quantities as Figures 4A–C ; ${\alpha }_1^T=2,{\alpha }_2^T=1,{\alpha }_3^T=1$ ; α^T is the nondimensional total Ag concentration (see Sec. 4.1.6).

Figure 8

Fraction of MBC#1 vs. number of sequential GC simulations for different initial affinity advantage values and different Ag#1 concentrations, with 10 total BCR/Epitope pairs. (A, B) MBC#1 fraction (ζ) at the end of simulations. (A) BCR#1 is cooperatively bivalent (K¹² _eq =10K¹¹ _eq); (B) BCR#1 is monovalent (K¹² _eq =0). The four sets of panels (A, B) show the effect of increasing occlusion from o=0 (no competition) to o=1 (full competition).