Generalized scaling of spin qubit coherence in over 12,000 host materials

Abstract

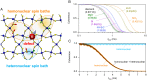
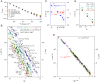
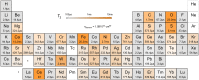
SignificanceAtomic defects in solid-state materials are promising candidates as quantum bits, or qubits. New materials are actively being investigated as hosts for new defect qubits; however, there are no unifying guidelines that can quantitatively predict qubit performance in a new material. One of the most critical property of qubits is their quantum coherence. While cluster correlation expansion (CCE) techniques are useful to simulate the coherence of electron spins in defects, they are computationally expensive to investigate broad classes of stable materials. Using CCE simulations, we reveal a general scaling relation between the electron spin coherence time and the properties of qubit host materials that enables rapid and quantitative exploration of new materials hosting spin defects.

Keywords: cluster correlation expansion; electron spin coherence; quantum information; scaling laws; spin qubits.

Fig. 1.

Quantum spin coherence simulation. (A) Schematic of CCE-2 of a defect electron spin in a heteronuclear compound. Arrows indicate nuclear (red and green) and electron (skyblue) spins with finite quantum numbers. (B) Hahn echo signal $\mathcal{L}(t_{\text{free}})$ versus free evolution time $t_{\text{free}}$ calculated by CCE-2 for naturally abundant isotopic diamond, 4H-SiC, silicon, and several oxides obtained by simulation under external magnetic field $B$ = 5 T. (C) $\mathcal{L}\left(t_{\text{free}}\right)$ of SiO₂ (α-quartz) with $B$ = 300 mT. In addition to the $\mathcal{L}\left(t_{\text{free}}\right)$ with dipole–dipole interactions with all baths (black), that with solely homonuclear spin bath (orange) and heteronuclear spins (blue) are shown. Error bars indicate the sample SD of the Hahn echo signal for different instances of nuclear spin coordinates.

Fig. 2.

Scaling of quantum coherence of decoupled spin baths. (A) Predicted quantum coherence time $T_2$ of defects in crystals composed of carbon as a function of ¹³C density $n_i$($i$ = ¹³C) with various crystal structures. The dashed line shows the fit to a power law $a_i{n}_i^{\mathit{\alpha }}$, with $a_i$ being coefficient, $\alpha$ the exponent −1.0. An external magnetic field of 5 T is applied along the [111] direction of the diamond structure and along [001] directions of other crystal structures. (B) Coefficient $a_i$ and corresponding $T_2$ with nuclear spin density $n_i$ = 1.0$\times$10²⁰ cm⁻³ as a function of the absolute value of nuclear spin g-factor $\mid g_i\mid$ calculated for all stable isotopes with the nuclear spin quantum number $I_i$. Lines are power law fits $T_{2,i}=b{\mid g_i\mid }^{\beta }$ on the different half-integer–$I_i$ spins. (C) Intercept $b$ versus $I_i$ with the power law fit $b=c{I}_i^{-1.10\pm 0.03}$ (blue), with $c$ being the coefficient, and the exponent $\beta$ versus $I_i$ with the theoretical value $\beta$ = −13/8 for $I_i$ = 1/2 (25, 27)) (red). (D) $T_2$ versus $\mid g_i\mid I_i{}^{0.66}$. The solid line is the power law fit. All simulations are conducted under external magnetic field of 5 T. (A–D) Electron g-factor $g_{\text{e}}$ = 2.0 and $S$ = 1/2 are assumed. (E) Coefficient $c$ for the transition of electron spin states between $\mid m_{\text{S}}^{-}\rangle \leftrightarrow \mid m_{\text{S}}^{+}\rangle$ as a function of $g_{\text{e}}$. Dashed lines are the power law fits. Error bars indicate the sample SD obtained by the simulation for different crystal coordinates for the isotopes (B, D). Error bars indicate the SE obtained from fitting the simulated CCE data (C, E).

Fig. 3.

Periodic table for quantum coherence. Coherence time $T_2$ based on CCE calculations for spin qubits in hypothetical material hosts with natural abundance of a single species with element density $n_{\text{element}}$ = 1.0$\times$10²³ cm⁻³ obtained by Eqs. 1 and 2 at the dilute limit assuming an electron spin g-factor of 2 and quantum number of 1/2. Hatched elements contain spinful nuclear spin density over the dilute limit $n_{\text{i}}$ ∼1.0$\times$10²² cm⁻³ at $n_{\text{element}}$ = 1.0$\times$10²³ cm⁻³. Note that diamond has one of the largest number densities in compounds with $n_{\text{C}}$ = 1.8$\times$10²³ cm⁻³, and $n_{\text{element}}$ of each element in compound is smaller than 1.0$\times$10²³ cm⁻³. The periodic table is color coded by $T_2$ on a log scale. Materials that are difficult to make compounds from (He, Ne, Ar) or that are without stable isotopes (Tc, Pm) are excluded.

Fig. 4.

Materials to explore. Types of 832 stable compounds with quantum coherence time $T_2$ longer than 1 ms and predicted bandgap larger than 1.0 eV. SiC is the only stable widegap nonchalcogenide with $T_2$ > 1 ms.