Fractional-Order Traveling Wave Approximations for a Fractional-Order Neural Field Model

Abstract

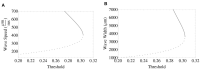
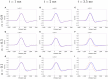
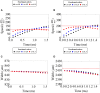
In this work, we establish a fractional-order neural field mathematical model with Caputo's fractional derivative temporal order α considering 0 < α < 2, to analyze the effect of fractional-order on cortical wave features observed preceding seizure termination. The importance of this incorporation relies on the theoretical framework established by fractional-order derivatives in which memory and hereditary properties of a system are considered. Employing Mittag-Leffler functions, we first obtain approximate fractional-order solutions that provide information about the initial wave dynamics in a fractional-order frame. We then consider the Adomian decomposition method to approximate pulse solutions in a wider range of orders and longer times. The former approach establishes a direct way to investigate the initial relationships between fractional-order and wave features, such as wave speed and wave width. In contrast, the latter approach displays wave propagation dynamics in different fractional orders for longer times. Using the previous two approaches, we establish approximate wave solutions with characteristics consistent with in vivo cortical waves preceding seizure termination. In our analysis, we find consistent differences in the initial effect of the fractional-order on the features of wave speed and wave width, depending on whether α <1 or α>1. Both cases can model the shape of cortical wave propagation for different fractional-orders at the cost of modifying the wave speed. Our results also show that the effect of fractional-order on wave width depends on the synaptic threshold and the synaptic connectivity extent. Fractional-order derivatives have been interpreted as the memory trace of the system. This property and the results of our analysis suggest that fractional-order derivatives and neuronal collective memory modify cortical wave features.

Keywords: cortical wave propagation; fractional-order derivative; memory effect; neural fields; traveling wave.

Figure 1

Traveling wave solutions for the first-order neural field model with wave features consistent with in vivo clinical features. (A) Wave speed determined by synaptic threshold k. (B) Wave width determined by synaptic threshold k. The lower branch (dashed gray curve) consists of unstable waves and the upper branch (gray curve), of stable waves colliding in a saddle-node bifurcation as the synaptic threshold is increased. Parameters used for these plots: ϵ = 0.1, β = 1 and σ = 1, 000 μm.

Figure 2

Fractional and integer-order traveling wave solutions u_⋆(x, t), q_⋆(x, t), u_⋆L(x, t), q_⋆L(x, t), u_⋆R(x, t), and q_⋆R(x, t). In this plot, we show the spatial wave profiles for a fixed initial time of t = 0. The solid gray lines correspond to the activity (leftmost wave) and adaptation (rightmost wave) in the integer-order case α = 1. The dotted red lines correspond to α = 0.99, the dashed red lines correspond to α = 0.9, the dotted blue lines correspond to α = 1.01, and the dashed blue lines correspond to α = 1.1. We consider two distinct traveling waves with similar features that are located in the upper (stable) branch to compare the effect of fractional-order on wave characteristics. For the integer-order α = 1, the wave speed is c = 402.8 μm/ms, the wave width is w = 3616.1 μm, and the synaptic threshold is k = 0.304. For the fractional-order α = 0.99, the wave speed is c = 405.1 μm/ms, the wave width is w = 3625.6 μm, and the synaptic threshold is k = 0.302. For the fractional-order α = 0.9, the wave speed is c = 433.8 μm/ms, the wave width is w = 3887.5 μm and the synaptic threshold is k = 0.292. For the fractional-order α = 1.01, the wave speed is c = 398.7μm/ms, the wave width is w = 3, 570 μm, and the synaptic threshold is k = 0.305. For the fractional-order α = 1.1, the wave speed is c = 379 μm/ms, the wave width is w = 3438.6 μm and the synaptic threshold k = 0.314. Parameters fixed for this plot: β = 1, ϵ = 0.1, and σ = 1, 000 μm.

Figure 3

Wave speed vs. synaptic threshold (A,B) and wave width vs. synaptic threshold (C,D). The values of the synaptic connectivity range include the following: for (A,C) σ = 1, 000 μm, and for (B,D) σ=1,500 μm. Gray lines correspond to the integer-order case α = 1, blue lines correspond to α ≈ 1⁺ (dashed lines α = 1.01, dotted lines α = 1.1), and red lines correspond to α ≈ 1⁻ (dashed lines α = 0.99, dotted lines α = 0.9). The gray rectangles determine the regions of interest near the upper (stable) branch that are suited for our explicit approximations considering the error estimates described in the Supplementary Material. We acknowledge that a big portion of the stable branch (not shown) cannot be analyzed by these approximations. In (A,B), we note that the effect of the order of the derivative in wave speed is to modify the synaptic threshold in which a fixed speed is achieved. For values α ≈ 1⁻, a fixed wave speed is achieved with less synaptic threshold compared to values of α ≈ 1⁺. In (C,D), we note that, in general, the effect of the order of the derivative in wave width is also to modify the synaptic threshold in which such a width is achieved. However, in this case, a nonlinear effect of the order of the derivative and extent of the synaptic connectivity on the lower branch is present. For values α ≈ 1⁻, a fixed wave width is achieved with less synaptic threshold compared to values of α ≈ 1⁺. Parameters fixed for these plots: β = 1 and ϵ = 0.1.

Figure 4

Wave width vs. wave speed for different fractional-order estimates and synaptic connectivity. Gray lines correspond to the integer-order case α = 1, blue lines correspond to α ≈ 1⁺ and red lines correspond to α ≈ 1⁻. Short dashes represent values of α closer to 1, that is, short red dashes represent α = 0.99 and short blue dashes represent α = 1.01. Large red dashes represent α = 0.9 and blue large dashes represent α = 1.1. The gray point, the red point and the blue point represent wave features for a fixed synaptic threshold of k = 0.2 for α = 1, α = 0.9, and α = 1.1, respectively. Similarly, the gray square, the red square, and the blue square represent the fixed synaptic threshold of k = 0.28. (A) We fix σ = 1, 000 μm. (B) We fix σ = 1, 500 μm. (A,B) We note that the relationship between wave width and fractional-order is not substantially affected for a wave with correspondent low synaptic threshold. We also observe that a fractional-order of α ≈ 1⁻ tends to increase wave width and wave speed relative to α = 1. On the other hand, α ≈ 1⁺ tends to decrease wave width and wave speed relative to α = 1. The previous analysis is valid for sufficiently wide waves, as observed in Figure 3. The wave features obtained for k = 0.2 (unstable branch) only modify wave speed. On the other hand, in considering k = 0.28 we observe an effect on both the width and the speed of the wave. This change is also affected by the synaptic connectivity range. Parameters fixed for all plots: β = 1 and ϵ = 0.1.

Figure 5

Wave speed and wave width as a function of time as estimated by the Adomian Decomposition Method in the case of 0 < α <1. (A,D) Wave speed vs. synaptic threshold and wave width vs. synaptic threshold, respectively. The gray rectangles determine the regions of interest in the upper (stable) branch that are suited for the Adomian Decomposition Method according to the error estimates established in the Supplementary Material (up to t = 2 ms). Here, we choose two distinct wave solutions to analyze the effect of fractional-order on wave features. The “red square solution” determines a wave solution considering k = 0.28 (c = 202 μm/ms and w = 2, 413 μm) and the “red circle solution” determines a wave solution considering k = 0.33 (c = 110 μ m/ms and w = 847 μm). (B,C,E,F) Wave speed and wave width for the wave solution as time evolves determined by the red circle solution (B,E) and red square solution (C,F), respectively. The different color dots determine distinct fractional-orders. The red dashed lines determine the features of the integer-order initial solution. (B,C) The fractional wave solutions present an initial increase in wave speed, in agreement with the Mittag-Leffler approximations, followed by a subsequent and significant decrease in wave speed. (E) The fractional wave solutions α ≈ 1 present an insignificant increase in wave width. (F) The fractional wave solutions present a slight increase in wave width. (A–F) Parameters fixed: ϵ = 0.1, β = 1.0, and σ = 300 μm.

Figure 6

Approximate fractional-order traveling pulse solutions using the Adomian decomposition method in the case of 0 < α <1. The dashed red curve denotes the integer-order initial pulse solution (Equation 5) determined by the “red square solution” and the blue curve denotes the approximate fractional pulse solution. Each row and column determine a different fractional-order and time as is described in the caption. (A–F) The effect of fractional-order on wave speed is nonlinear. In all cases, there is an initial increase of wave speed, followed by a decrease in wave speed. On the other hand, for all fractional orders and all times, we find a consistent and slight increase in wave width as is described in Figure 5. The fractional-order approximations provide an insight of a possible effect of fractional-order on wave profile finding a slight change in the wave amplitude. (A–F) Parameters fixed: ϵ = 0.1, β = 1.0, k = 0.33 and σ = 300 μm.

Figure 7

Approximate fractional-order traveling pulse solutions using the Adomian decomposition method in the case of 0 < α <1. The dashed red curve denotes the integer-order initial pulse solution (Equation 5) determined by the “red circle solution” and the blue curve denotes the approximate fractional pulse solution. Each row and column determine a different fractional-order and time as is described in the caption. (A–I) The effect of fractional-order on wave speed is nonlinear. In all cases, there is an initial increase of wave speed, followed by a decrease in wave speed. The fractional-order approximations provide an insight of a possible effect of fractional-order on wave profile finding a slight increase in the wave amplitude. (A–I) Parameters fixed: ϵ = 0.1, β = 1.0, k = 0.28 and σ = 300 μm.

Figure 8

Approximate fractional-order traveling pulse solutions with different fractional orders using the Adomian decomposition method on the unstable branch considering the case of 0 < α <1. The dashed red curve denotes the explicit integer-order pulse solution (Equation 5). The dashed green line denotes the synaptic threshold, the blue curve denotes the fractional pulse, and the red dots determine the points at which the synaptic threshold is achieved. Each row and column determines a different fractional order and time. (A) Fractional-order α = 0.9 at time t = 1, we note a slight decrease in wave speed and slight decrease in wave width. (B) Fractional-order α = 0.9 at t = 2, the fractional pulse solution is no longer above the synaptic threshold, hence it is no longer considered a pulse solution. (C,D) Fractional-order α = 0.1 at time t = 1 and time t = 2, respectively. Similarly to (C), the fractional pulse solution is no longer above the synaptic threshold. (A–D) Parameters fixed: ϵ = 0.1, β = 1.5, k = 0.25 and σ = 500 μm. Initial wave features c = 160 μm/ms and w = 589 μm.

Figure 9

Wave speed and wave width as a function of time as estimated by the Adomian Decomposition Method in the case of 1 < α < 2. (A–D) Wave speed and wave width for the wave solution determined by the “red circle solution” (A,C) and “red square solution” (B,D), respectively. The different color dots determine distinct fractional-orders. The red dashed lines determine the features of the integer-order solutions initial solution. We analyze up to t = 1.5 in correspondence to the error estimates established in the Supplementary Material. (A,B) The fractional wave solutions present an initial decrease in wave speed, in agreement with the Mittag-Leffler approximations, followed by a subsequent increase in wave speed. (C) The fractional wave solutions present an insignificant decrease in wave width. (D) The fractional wave solutions present a slight decrease in wave width. A similar analysis has been made for longer synaptic connectivity ranges obtaining qualitatively similar results. (A–D) Parameters fixed: ϵ = 0.1, β = 1.0, and σ = 300 μm.

Figure 10

Approximate fractional-order traveling pulse solutions using the Adomian decomposition method in the case of 1 < α < 2. The dashed red curve denotes the integer-order initial pulse solution (Equation 5) determined by the “red square solution” and the blue curve denotes the approximate fractional pulse solution. Each row and column determine a different fractional-order and time as is described in the caption. (A–F) The effect of fractional-order on wave speed is nonlinear. In all cases, there is an initial decrease of wave speed, followed by an increase in wave speed. On the other hand, for all fractional orders and all times, we find a consistent and slight decrease in wave width as is described in Figure 9. The fractional-order approximations provide an insight of a possible effect of fractional-order on wave profile. (A–F) Parameters fixed: ϵ = 0.1, β = 1.0, k = 0.28 and σ = 300 μm.