Fractional-Order Traveling Wave Approximations for a Fractional-Order Neural Field Model
- PMID: 35399918
- PMCID: PMC8987931
- DOI: 10.3389/fncom.2022.788924
Fractional-Order Traveling Wave Approximations for a Fractional-Order Neural Field Model
Abstract
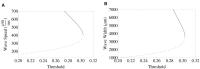
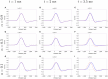
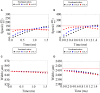
In this work, we establish a fractional-order neural field mathematical model with Caputo's fractional derivative temporal order α considering 0 < α < 2, to analyze the effect of fractional-order on cortical wave features observed preceding seizure termination. The importance of this incorporation relies on the theoretical framework established by fractional-order derivatives in which memory and hereditary properties of a system are considered. Employing Mittag-Leffler functions, we first obtain approximate fractional-order solutions that provide information about the initial wave dynamics in a fractional-order frame. We then consider the Adomian decomposition method to approximate pulse solutions in a wider range of orders and longer times. The former approach establishes a direct way to investigate the initial relationships between fractional-order and wave features, such as wave speed and wave width. In contrast, the latter approach displays wave propagation dynamics in different fractional orders for longer times. Using the previous two approaches, we establish approximate wave solutions with characteristics consistent with in vivo cortical waves preceding seizure termination. In our analysis, we find consistent differences in the initial effect of the fractional-order on the features of wave speed and wave width, depending on whether α <1 or α>1. Both cases can model the shape of cortical wave propagation for different fractional-orders at the cost of modifying the wave speed. Our results also show that the effect of fractional-order on wave width depends on the synaptic threshold and the synaptic connectivity extent. Fractional-order derivatives have been interpreted as the memory trace of the system. This property and the results of our analysis suggest that fractional-order derivatives and neuronal collective memory modify cortical wave features.
Keywords: cortical wave propagation; fractional-order derivative; memory effect; neural fields; traveling wave.
Copyright © 2022 González-Ramírez.
Conflict of interest statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures







References
-
- Abbaoui K., Cherruault Y. (1995). New ideas for proving convergence of decomposition methods. Comput. Math. Appl. 29, 103–108. 10.1016/0898-1221(95)00022-Q - DOI
-
- Abbasbandy A. (2007). The application of homotopy analysis method to solve a generalized hirota-satsuma coupled kdv equation. Phys. Lett. A 361, 478–483. 10.1016/j.physleta.2006.09.105 - DOI
-
- Adomian G. (1988). A review of the decomposition method in applied mathematics. J. Math. Anal. Appl. 135, 501–544. 10.1016/0022-247X(88)90170-9 - DOI
-
- Adomian G. (1994). Solving Frontier Problems of Physics: The Decomposition Method. Boston, MA: Kluwer Academic Publishers.
-
- Armanyos M., Radwan A. (2016). “Fractional-order fitzhugh-nagumo and izhikevich neuron models,” in 2016 13th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON) (Chiang Mai: IEEE; ), 1–5.
LinkOut - more resources
Full Text Sources

