Maximal Dependence Capturing as a Principle of Sensory Processing
- PMID: 35399919
- PMCID: PMC8989953
- DOI: 10.3389/fncom.2022.857653
Maximal Dependence Capturing as a Principle of Sensory Processing
Abstract
Sensory inputs conveying information about the environment are often noisy and incomplete, yet the brain can achieve remarkable consistency in recognizing objects. Presumably, transforming the varying input patterns into invariant object representations is pivotal for this cognitive robustness. In the classic hierarchical representation framework, early stages of sensory processing utilize independent components of environmental stimuli to ensure efficient information transmission. Representations in subsequent stages are based on increasingly complex receptive fields along a hierarchical network. This framework accurately captures the input structures; however, it is challenging to achieve invariance in representing different appearances of objects. Here we assess theoretical and experimental inconsistencies of the current framework. In its place, we propose that individual neurons encode objects by following the principle of maximal dependence capturing (MDC), which compels each neuron to capture the structural components that contain maximal information about specific objects. We implement the proposition in a computational framework incorporating dimension expansion and sparse coding, which achieves consistent representations of object identities under occlusion, corruption, or high noise conditions. The framework neither requires learning the corrupted forms nor comprises deep network layers. Moreover, it explains various receptive field properties of neurons. Thus, MDC provides a unifying principle for sensory processing.
Keywords: computational modeling; grandmother cell; invariant representation; object recognition (OR); redundancy capturing; redundancy reduction; sparse coding; sparse recovery (SR).
Copyright © 2022 Raj, Dahlen, Duyck and Yu.
Conflict of interest statement
RR, DD, and CRY declare the existence of a financial competing interest in the form of a patent application based on this work. The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures

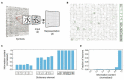


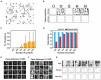
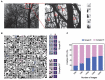
Similar articles
-
Representation and integration of multiple sensory inputs in primate superior colliculus.J Neurophysiol. 1996 Aug;76(2):1246-66. doi: 10.1152/jn.1996.76.2.1246. J Neurophysiol. 1996. PMID: 8871234
-
Learning optimized features for hierarchical models of invariant object recognition.Neural Comput. 2003 Jul;15(7):1559-88. doi: 10.1162/089976603321891800. Neural Comput. 2003. PMID: 12816566
-
Local minimization of prediction errors drives learning of invariant object representations in a generative network model of visual perception.Front Comput Neurosci. 2023 Sep 25;17:1207361. doi: 10.3389/fncom.2023.1207361. eCollection 2023. Front Comput Neurosci. 2023. PMID: 37818157 Free PMC article.
-
From sensation to cognition.Brain. 1998 Jun;121 ( Pt 6):1013-52. doi: 10.1093/brain/121.6.1013. Brain. 1998. PMID: 9648540 Review.
-
Learning Invariant Object and Spatial View Representations in the Brain Using Slow Unsupervised Learning.Front Comput Neurosci. 2021 Jul 21;15:686239. doi: 10.3389/fncom.2021.686239. eCollection 2021. Front Comput Neurosci. 2021. PMID: 34366818 Free PMC article. Review.
References
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

