Rotational dynamics and transition mechanisms of surface-adsorbed proteins
- PMID: 35412902
- PMCID: PMC9169768
- DOI: 10.1073/pnas.2020242119
Rotational dynamics and transition mechanisms of surface-adsorbed proteins
Abstract
Assembly of biomolecules at solid–water interfaces requires molecules to traverse complex orientation-dependent energy landscapes through processes that are poorly understood, largely due to the dearth of in situ single-molecule measurements and statistical analyses of the rotational dynamics that define directional selection. Emerging capabilities in high-speed atomic force microscopy and machine learning have allowed us to directly determine the orientational energy landscape and observe and quantify the rotational dynamics for protein nanorods on the surface of muscovite mica under a variety of conditions. Comparisons with kinetic Monte Carlo simulations show that the transition rates between adjacent orientation-specific energetic minima can largely be understood through traditional models of in-plane Brownian rotation across a biased energy landscape, with resulting transition rates that are exponential in the energy barriers between states. However, transitions between more distant angular states are decoupled from barrier height, with jump-size distributions showing a power law decay that is characteristic of a nonclassical Levy-flight random walk, indicating that large jumps are enabled by alternative modes of motion via activated states. The findings provide insights into the dynamics of biomolecules at solid–liquid interfaces that lead to self-assembly, epitaxial matching, and other orientationally anisotropic outcomes and define a general procedure for exploring such dynamics with implications for hybrid biomolecular–inorganic materials design.
Keywords: Levy-flight transition; high-speed atomic force microscopy; machine learning; orientational energy landscapes; rotational dynamics of protein.
Conflict of interest statement
The authors declare no competing interest.
Figures
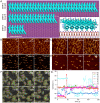
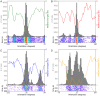


References
-
- Kerfeld C. A., et al. , Protein structures forming the shell of primitive bacterial organelles. Science 309, 936–938 (2005). - PubMed
-
- Yeates T. O., Kerfeld C. A., Heinhorst S., Cannon G. C., Shively J. M., Protein-based organelles in bacteria: Carboxysomes and related microcompartments. Nat. Rev. Microbiol. 6, 681–691 (2008). - PubMed
-
- Pfeifer F., Distribution, formation and regulation of gas vesicles. Nat. Rev. Microbiol. 10, 705–715 (2012). - PubMed
-
- Weissbuch I., Addadi L., Lahav M., Leiserowitz L., Molecular recognition at crystal interfaces. Science 253, 637–645 (1991). - PubMed

