Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 Mar 22;24(4):436.
doi: 10.3390/e24040436.

A Quantitative Comparison between Shannon and Tsallis-Havrda-Charvat Entropies Applied to Cancer Outcome Prediction

Thibaud Brochet  1 , Jérôme Lapuyade-Lahorgue  1 , Alexandre Huat  1   2   3 , Sébastien Thureau  1   2 , David Pasquier  4 , Isabelle Gardin  1   2 , Romain Modzelewski  1   2 , David Gibon  3 , Juliette Thariat  5 , Vincent Grégoire  6 , Pierre Vera  1   2 , Su Ruan  1
Affiliations

A Quantitative Comparison between Shannon and Tsallis-Havrda-Charvat Entropies Applied to Cancer Outcome Prediction

Thibaud Brochet et al. Entropy (Basel). .

Erratum in

Abstract

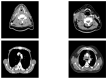
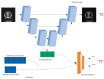
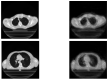
In this paper, we propose to quantitatively compare loss functions based on parameterized Tsallis-Havrda-Charvat entropy and classical Shannon entropy for the training of a deep network in the case of small datasets which are usually encountered in medical applications. Shannon cross-entropy is widely used as a loss function for most neural networks applied to the segmentation, classification and detection of images. Shannon entropy is a particular case of Tsallis-Havrda-Charvat entropy. In this work, we compare these two entropies through a medical application for predicting recurrence in patients with head-neck and lung cancers after treatment. Based on both CT images and patient information, a multitask deep neural network is proposed to perform a recurrence prediction task using cross-entropy as a loss function and an image reconstruction task. Tsallis-Havrda-Charvat cross-entropy is a parameterized cross-entropy with the parameter α. Shannon entropy is a particular case of Tsallis-Havrda-Charvat entropy for α=1. The influence of this parameter on the final prediction results is studied. In this paper, the experiments are conducted on two datasets including in total 580 patients, of whom 434 suffered from head-neck cancers and 146 from lung cancers. The results show that Tsallis-Havrda-Charvat entropy can achieve better performance in terms of prediction accuracy with some values of α.

Keywords: Shannon entropy; Tsallis–Havrda–Charvat entropy; deep neural networks; generalized entropies; head–neck cancer; lung cancer; recurrence prediction.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Input images: head–neck CT (above) and lung CT (below).
Figure 2
Figure 2
Architecture of the multitask neural network for recurrence prediction (T2) with the help of another task (T1: image reconstruction).
Figure 3
Figure 3
Input images: original images (left) vs. reconstructed images (right).
See this image and copyright information in PMC

References

    1. Wang Q., Ma Y., Zhao K., Tian Y. A Comprehensive Survey of Loss Functions in Machine Learning. Ann. Data Sci. 2020;9:187–212. doi: 10.1007/s40745-020-00253-5. - DOI
    1. Chung J.K., Kannappan C.T., Sahoo P.K. Measures of distance between probability distributions. J. Math. Anal. Appl. 1989;138:280–292. doi: 10.1016/0022-247X(89)90335-1. - DOI
    1. Budzynski R.J., Kontracki W., Krolak A. Applications of distance between distributions to gravitational wave data analysis. Class. Quantum Gravity. 2007;25:015005. doi: 10.1088/0264-9381/25/1/015005. - DOI
    1. Serrurier M. An informational distance for estimating the faithfulness of a possibility distribution, viewed as a family of probability distributions, with respect to data. Int. J. Approx. Reason. 2013;54:919–933. doi: 10.1016/j.ijar.2013.01.011. - DOI
    1. Kullback S., Leibler R.A. On information and sufficiency. Ann. Math. Stat. 1951;22:79–86. doi: 10.1214/aoms/1177729694. - DOI

LinkOut - more resources