Epistemic Communities under Active Inference
- PMID: 35455140
- PMCID: PMC9027706
- DOI: 10.3390/e24040476
Epistemic Communities under Active Inference
Abstract
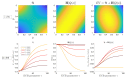
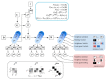
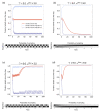
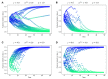
The spread of ideas is a fundamental concern of today's news ecology. Understanding the dynamics of the spread of information and its co-option by interested parties is of critical importance. Research on this topic has shown that individuals tend to cluster in echo-chambers and are driven by confirmation bias. In this paper, we leverage the active inference framework to provide an in silico model of confirmation bias and its effect on echo-chamber formation. We build a model based on active inference, where agents tend to sample information in order to justify their own view of reality, which eventually leads to them to have a high degree of certainty about their own beliefs. We show that, once agents have reached a certain level of certainty about their beliefs, it becomes very difficult to get them to change their views. This system of self-confirming beliefs is upheld and reinforced by the evolving relationship between an agent's beliefs and observations, which over time will continue to provide evidence for their ingrained ideas about the world. The epistemic communities that are consolidated by these shared beliefs, in turn, tend to produce perceptions of reality that reinforce those shared beliefs. We provide an active inference account of this community formation mechanism. We postulate that agents are driven by the epistemic value that they obtain from sampling or observing the behaviours of other agents. Inspired by digital social networks like Twitter, we build a generative model in which agents generate observable social claims or posts (e.g., 'tweets') while reading the socially observable claims of other agents that lend support to one of two mutually exclusive abstract topics. Agents can choose which other agent they pay attention to at each timestep, and crucially who they attend to and what they choose to read influences their beliefs about the world. Agents also assess their local network's perspective, influencing which kinds of posts they expect to see other agents making. The model was built and simulated using the freely available Python package pymdp. The proposed active inference model can reproduce the formation of echo-chambers over social networks, and gives us insight into the cognitive processes that lead to this phenomenon.
Keywords: active inference; epistemic community; opinion dynamics; social media.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
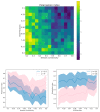
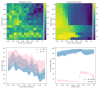
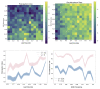
References
-
- Henrich J. Culture and social behavior. Curr. Opin. Behav. Sci. 2015;3:84–89. doi: 10.1016/j.cobeha.2015.02.001. - DOI
-
- Heerwagen J.H., Orians G.H. Humans, habitats. Biophilia Hypothesis. 1995;138:138–172.
-
- Lau R.R., Redlawsk D.P. Advantages and disadvantages of cognitive heuristics in political decision making. Am. J. Political Sci. 2001;45:951–971. doi: 10.2307/2669334. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

