A Light-Powered Liquid Crystal Elastomer Spring Oscillator with Self-Shading Coatings

Abstract

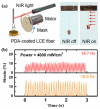
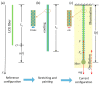
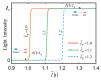
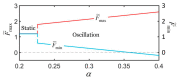
The self-oscillating systems based on stimuli-responsive materials, without complex controllers and additional batteries, have great application prospects in the fields of intelligent machines, soft robotics, and light-powered motors. Recently, the periodic oscillation of an LCE fiber with a mass block under periodic illumination was reported. This system requires periodic illumination, which limits the application of self-sustained systems. In this paper, we creatively proposed a light-powered liquid crystal elastomer (LCE) spring oscillator with self-shading coatings, which can self-oscillate continuously under steady illumination. On the basis of the well-established dynamic LCE model, the governing equation of the LCE spring oscillator is formulated, and the self-excited oscillation is studied theoretically. The numerical calculations show that the LCE spring oscillator has two motion modes, static mode and oscillation mode, and the self-oscillation arises from the coupling between the light-driven deformation and its movement. Furthermore, the contraction coefficient, damping coefficient, painting stretch, light intensity, spring constant, and gravitational acceleration all affect the self-excited oscillation of the spring oscillator, and each parameter is a critical value for triggering self-excited oscillation. This work will provide effective help in designing new optically responsive structures for engineering applications.

Keywords: light-powered mechanisms; limit cycles; liquid crystal elastomer; self-shading effect; spring oscillator.

Figure 1

Periodic oscillation of an LCE fiber with a mass block in a periodic illumination [10]. (a) Schematic diagram; (b) dependence of the strain of LCE fiber against time for two different frequencies of illumination.

Figure 2

Schematic of an optically responsive LCE spring oscillator made of a mass block and an LCE fiber coated with an opaque powder coating under steady and homogeneous illumination. (a) Reference configuration of the LCE fiber; (b) the LCE fiber is pre-stretched to the length of $L_{\mathrm{p}}$ (we call it painting stretch) and painted with an opaque powder coating; (c) the current configuration of the spring oscillator. Under stable illumination, the coupling of light-driven LCE fiber contraction and movement of the mass block can trigger self-sustaining oscillation.

Figure 3

The shading effect of shading coating. For $l\left(t\right)>L_{\mathrm{p}}$, the LCE fiber is in an illuminated state. For $l\left(t\right)\le L_{\mathrm{p}}$, the LCE fiber is in a non-illuminated state. The self-excited oscillation of the mass block can be triggered under uniform and constant illumination due to the self-shading effect of the coating.

Figure 4

Two motion modes of the LCE spring oscillator: (a,b) Static state ($\tilde{c}=0.38$); (c,d) oscillation state ($\tilde{c}=0.26$). The other dimensionless parameters are: $\tilde{I}=0.35$, $\tilde{k}=5.8$, $\alpha =0.23$, $\tilde{g}=1.2$, ${\tilde{L}}_{\mathrm{p}}=1.1$, ${\tilde{u}}_0=0$, and ${\tilde{\dot{u}}}_0=0$.

Figure 5

Mechanism of self-excited oscillation of the LCE spring oscillator. (a) The change in the cis number fraction of LCE fiber with time; (b) the photo-triggered contraction strain of LCE fiber over time; (c) the dependence of the driving force on time; (d) the relationship between the driving force and the displacement. The parameters are set as $\tilde{I}=0.38$, $\tilde{k}=5.8$, $\tilde{c}=0.28$, $\alpha =0.25$, $\tilde{g}=1.2$, ${\tilde{L}}_{\mathrm{p}}=1.1$, ${\tilde{u}}_0=0$, and ${\tilde{\dot{u}}}_0=0$.

Figure 6

Dependence of maximum and minimum dimensionless spring force on the contraction coefficient. The parameters are $\tilde{I}=0.32$, $\tilde{k}=5.8$, $\tilde{c}=0.23$, $\tilde{g}=1.2$, ${\tilde{L}}_{\mathrm{p}}=1.1$, ${\tilde{u}}_0=0$, and ${\tilde{\dot{u}}}_0=0$.

Figure 7

The effect of the contraction coefficient on self-excited oscillation for given values of $\tilde{I}=0.32$, $\tilde{k}=5.8$, $\tilde{c}=0.23$, $\tilde{g}=1.2$, ${\tilde{L}}_{\mathrm{p}}=1.1$, ${\tilde{u}}_0=0$, and ${\tilde{\dot{u}}}_0=0$. (a) Limit cycles; (b) amplitude, period, and equilibrium position. There exists a critical contraction coefficient $\alpha =-0.227$ for triggering self-excited oscillation.

Figure 8

The effect of the damping coefficient on self-excited oscillation for $\tilde{I}=0.32$, $\tilde{k}=5.8$, $\alpha =0.25$, $\tilde{g}=1.2$, ${\tilde{L}}_{\mathrm{p}}=1.1$, ${\tilde{u}}_0=0$, and ${\tilde{\dot{u}}}_0=0$. (a) Limit cycles; (b) amplitude, period, and equilibrium position. There exists a critical damping coefficient $\tilde{c}=0.275$ for triggering self-excited oscillation.

Figure 9

The effect of painting stretch on self-excited oscillation for $\tilde{I}=0.3$, $\tilde{k}=5.8$, $\alpha =0.35$, $\tilde{g}=1.2$, $\tilde{c}=0.27$, ${\tilde{u}}_0=0$, and ${\tilde{\dot{u}}}_0=0$. (a) Limit cycles; (b) amplitude, period, and equilibrium position.

Figure 10

The effect of light intensity on self-excited oscillation for $\tilde{k}=5.8$, $\tilde{c}=0.28$, $\alpha =0.3$, $\tilde{g}=1.2$, ${\tilde{L}}_{\mathrm{p}}=1.1$, ${\tilde{u}}_0=0$, and ${\tilde{\dot{u}}}_0=0$. (a) Limit cycles; (b) amplitude, period, and equilibrium position. There exists a critical light intensity $\tilde{I}=0.223$ for triggering self-excited oscillation.

Figure 11

The effect of the spring constant on self-excited oscillation for $\tilde{I}=0.32$, $\tilde{c}=0.28$, $\alpha =0.3$, $\tilde{g}=1.2$, ${\tilde{L}}_{\mathrm{p}}=1.1$, ${\tilde{u}}_0=0$, and ${\tilde{\dot{u}}}_0=0$. (a) Limit cycles; (b) amplitude, period, and equilibrium position. There exists a critical spring constant $\tilde{k}=5.4$ for triggering self-excited oscillation.

Figure 12

The effect of gravitational acceleration on self-excited oscillation for given values of $\tilde{k}=5.8$, $\tilde{c}=0.24$, $\alpha =-0.25$, $\tilde{I}=0.32$, ${\tilde{L}}_{\mathrm{p}}=1.1$, ${\tilde{u}}_0=0$, and ${\tilde{\dot{u}}}_0=0$. (a) Limit cycles; (b) amplitude, period, and equilibrium position. There exists a critical gravitational acceleration $\tilde{g}=1.24$ for triggering self-excited oscillation.

Figure 13

The effect of initial conditions on self-excited oscillation for $\tilde{I}=0.23$, $\tilde{k}=5.8$, $\tilde{c}=0.36$, $\alpha =0.26$, $\tilde{g}=1.2$, ${\tilde{L}}_{\mathrm{p}}=1.15$, and ${\tilde{u}}_0=0$. (a) Limit cycles; (b) amplitude, period, and equilibrium position. The initial velocity does not affect the self-excited oscillation.