Investigation of a time-fractional COVID-19 mathematical model with singular kernel

Abstract

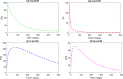
We investigate the fractional dynamics of a coronavirus mathematical model under a Caputo derivative. The Laplace-Adomian decomposition and Homotopy perturbation techniques are applied to attain the approximate series solutions of the considered system. The existence and uniqueness solution of the system are presented by using the Banach fixed-point theorem. Ulam-Hyers-type stability is investigated for the proposed model. The obtained approximations are compared with numerical simulations of the proposed model as well as associated real data for numerous fractional-orders. The results reveal a good comparison between the numerical simulations versus approximations of the considered model. Further, one can see good agreements are obtained as compared to the classical integer order.

Keywords: Caputo fractional operator; Homotopy perturbation method; Laplace–Adomian decomposition method; Mathematical model of COVID-19; Ulam–Hyers stability.

Figure 1

Dynamical behavior of ${\mathbf{S}}_h(t)$, ${\mathbf{I}}_h(t)$, ${\mathbf{R}}_h(t)$ and $\mathbf{W}(t)$ at fractional-order $p=0.75$

Figure 2

Dynamical behavior of ${\mathbf{S}}_h(t)$, ${\mathbf{I}}_h(t)$, ${\mathbf{R}}_h(t)$ and $\mathbf{W}(t)$ at fractional-order $p=0.75$

Figure 3

Dynamical behavior of ${\mathbf{S}}_h(t)$, ${\mathbf{I}}_h(t)$, ${\mathbf{R}}_h(t)$ and $\mathbf{W}(t)$ at fractional-order $p=0.85$

Figure 4

Dynamical behavior of ${\mathbf{S}}_h(t)$, ${\mathbf{I}}_h(t)$, ${\mathbf{R}}_h(t)$ and $\mathbf{W}(t)$ at fractional-order $p=0.85$

Figure 5

Dynamical behavior of ${\mathbf{S}}_h(t)$, ${\mathbf{I}}_h(t)$, ${\mathbf{R}}_h(t)$ and $\mathbf{W}(t)$ at fractional-order $p=0.95$

Figure 6

Dynamical behavior of ${\mathbf{S}}_h(t)$, ${\mathbf{I}}_h(t)$, ${\mathbf{R}}_h(t)$ and $\mathbf{W}(t)$ at fractional-order $p=0.95$

Figure 7

Dynamical behavior of ${\mathbf{S}}_h(t)$, ${\mathbf{I}}_h(t)$, ${\mathbf{R}}_h(t)$ and $\mathbf{W}(t)$ at integer order $p=1$

Figure 8

Dynamical behavior of ${\mathbf{S}}_h(t)$, ${\mathbf{I}}_h(t)$, ${\mathbf{R}}_h(t)$ and $\mathbf{W}(t)$ at integer order $p=1$