Bio-Inspired Propulsion: Towards Understanding the Role of Pectoral Fin Kinematics in Manta-like Swimming

Abstract

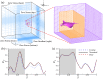
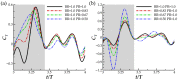
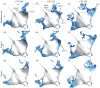
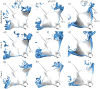
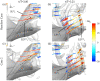
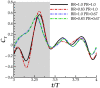
Through computational fluid dynamics (CFD) simulations of a model manta ray body, the hydrodynamic role of manta-like bioinspired flapping is investigated. The manta ray model motion is reconstructed from synchronized high-resolution videos of manta ray swimming. Rotation angles of the model skeletal joints are altered to scale the pitching and bending, resulting in eight models with different pectoral fin pitching and bending ratios. Simulations are performed using an in-house developed immersed boundary method-based numerical solver. Pectoral fin pitching ratio (PR) is found to have significant implications in the thrust and efficiency of the manta model. This occurs due to more optimal vortex formation and shedding caused by the lower pitching ratio. Leading edge vortexes (LEVs) formed on the bottom of the fin, a characteristic of the higher PR cases, produced parasitic low pressure that hinders thrust force. Lowering the PR reduces the influence of this vortex while another LEV that forms on the top surface of the fin strengthens it. A moderately high bending ratio (BR) can slightly reduce power consumption. Finally, by combining a moderately high BR = 0.83 with PR = 0.67, further performance improvements can be made. This enhanced understanding of manta-inspired propulsive mechanics fills a gap in our understanding of the manta-like mobuliform locomotion. This motivates a new generation of manta-inspired robots that can mimic the high speed and efficiency of their biological counterpart.

Keywords: batoid-like swimming; bio-inspired locomotion; high-fidelity flow simulation; manta ray.

Figure 1

Comparison between biological motion and prescribed manta-like motion from side (a) and back (b) views at T = 0.33. (c) Skeletal joint arrangement for the current model.

Figure 2

(a) Geometric variables for the manta ray model along with fin tip trajectories illustrating manta-like flapping motion during the downstroke (red trajectory) and upstroke (blue trajectory); (b) fin tip y-displacement.

Figure 3

Comparison of (a) θ_P and (b) θ_B at pectoral fin span s/S = 0.5 for three PR and BR combinations.

Figure 4

(a) Schematic of the computational domain and boundary conditions used in the present study. (b) Instantaneous thrust and (c) lift comparison between the coarse mesh (∆ = 0.018 BL, ~4.3 million nodes) nominal mesh (∆ = 0.0085 BL, ~8.7 million nodes), and fine mesh (∆ = 0.0065 BL, ~15.4 million nodes).

Figure 5

Illustration of Poisson equation pressure convergence for 3 time steps during a cycle of motion: T = 0.33 (320th time step), T = 0.66 (640th time step), and T = 1.0 (960th time step).

Figure 6

Instantaneous C_T for (a) the baseline case (BR = 1.0 PR = 1.0), case 1 (BR = 1.0 PR = 0.83), case 2 (BR = 1.0 PR = 0.67) and case 3 (BR = 1.0 PR = 0.50); (b) the baseline case (BR = 1.0 PR = 1.0), case 4 (BR = 0.80 PR = 1.0), case 2 (BR = 0.67 PR = 1.0) and case 3 (BR = 0.50 PR = 1.0).

Figure 7

Perspective views of downstroke vortex formation for the baseline case (BR = 1.0 PR = 1.0) (a–c) case 3 (BR = 1.0 PR = 0.50) (d–f) and case 6 (BR = 0.5 PR = 1.0) (g–i) at t/T = 3.08 (a,d,g) t/T = 3.21 (b,e,h) and t/T = 3.43 (c,f,i).

Figure 8

Perspective views of upstroke vortex formation for the baseline case (BR = 1.0 PR = 1.0) (a–c) case 3 (BR = 1.0 PR = 0.50) (d–f) and case 6 (BR = 0.5 PR = 1.0) (g–i) at t/T = 3.53 (a,d,g) t/T = 3.77 (b,e,h) and t/T = 4.0 (c,f,i).

Figure 9

Spanwise vorticity plots for the baseline case (BR = 1.0 PR = 1.0) (a,b) and case 2 (BR = 1.0 PR = 0.67) (c,d) at t/T = 3.0 (a,c) and t/T = 3.21 (b,d).

Figure 10

Baseline case (BR = 1.0 PR = 1.0) (a) Vorticity magnitude at half downstroke with (b,c) resulting surface pressure on top and bottom, respectively.

Figure 11

Case 2 (BR = 1.0 PR = 0.67) (a) Vorticity magnitude at half downstroke with (b,c) resulting surface pressure on top and bottom, respectively.

Figure 12

Instantaneous thrust performance comparison for newly added case 7 with BR = 0.83 PR = 0.67.

Figure 13

(a) Illustration of location of slice cuts relative to the manta body with downstroke motion (red trajectory) and upstroke motion (blue trajectory) visualized; (b,c) baseline case (BR = 1.0 PR = 1.0) and (d,e) case 7 (BR = 0.83 PR = 0.67) mean flow at slice cuts.